Cuadrados mínimos

Para realizar un ajuste de una función por cuadrados mínimos, vamos a usar la función curve_fit de scipy.optimize.

Truco

Pueden utilizar el paquete labo1 que simplifica mucho el código para ajustar y realizar gráficos. Pueden ver la documentación en https://maurosilber.github.io/labo1.

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit

plt.rc("figure", dpi=100)

Nota

Hay funciones especializadas para casos particulares, como los casos lineales, que son más eficientes.

Motivación

Supongamos que tenemos una serie de \(N\) mediciones \((x_i, y_i)\), y sabemos que están relacionadas por una dada función \(f\):

\[ y = f(x, p_1, \ldots, p_k) \]

donde \(p_1, \ldots, p_k\) son parámetros de la función que queremos determinar.

Por ejemplo, supongamos que la función es \(y = Ax\), y queremos determinar el parámetro \(A\) a partir de los siguientes datos:

x = np.array([1, 2, 3, 4, 5])
y = 3 * x  # la constante A es 3!

plt.plot(x, y, marker="o")

[<matplotlib.lines.Line2D at 0x7fe2e427fa30>]

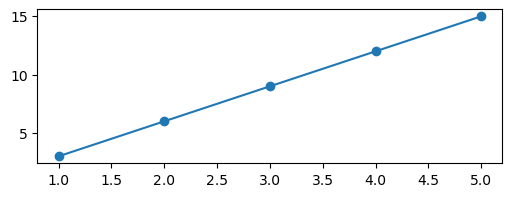
En este caso, alcanzaría con dividir \(y/x\) para obtener \(A\):

y / x

array([3., 3., 3., 3., 3.])

Pero, estas «mediciones» son perfectas, sin ninguna incerteza. En la práctica, todas las mediciones tienen un error.

Simulemos una medición agregándole error a los datos:

y_error = 1  # la desviación estándar
y_medido = np.random.normal(y, scale=y_error)

plt.plot(x, y, label="Ideal")
plt.scatter(x, y_medido, label="Medido")
plt.legend()

<matplotlib.legend.Legend at 0x7fe2d83b4430>

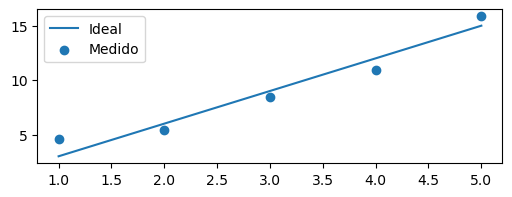
Si tratamos de determinar \(A\) a partir de estas mediciones, no obtenemos exactamente \(3\):

y_medido / x

array([4.62434536, 2.69412179, 2.82394275, 2.73175784, 3.17308153])

Obtenemos una pendiente \(A\) distinta para cada medición. ¿Cómo podemos unificarlas?

Una opción «incorrecta» para combinarlas es hacer un promedio de estos valores:

np.mean(y_medido / x)

3.2094498552819224

Pero hay una manera más general de resolver este problema, que es realizar un ajuste por cuadrados mínimos.

Ajuste por cuadrados mínimos

Para realizar un ajuste por cuadrados mínimos, vamos a usar la función curve_fit de scipy.optimize.

curve_fit necesita (al menos) 3 parámetros:

1. f, la función que queremos ajustar,

2. xdata, el array de datos en \(x\),

3. ydata, el array de datos en \(y\).

Importante

Es importante el orden de los parámetros al definir f. Primero va la variable x, y después los parámetros a determinar.

def lineal(x, A):
    return A * x


p_opt, p_cov = curve_fit(lineal, x, y_medido)

p_opt, p_cov

(array([2.97911784]), array([[0.02349053]]))

curve_fit devuelve dos valores:

• p_opt es un array que contiene los valores óptimos de los parámetros,

• p_cov es la matriz de covarianza de los parámetros.

En este caso,

• p_opt es un array de tamaño \(1\) que contiene el valor óptimo de \(A\),

• p_cov es una matriz de \(1\times1\) que contiene la varianza de \(A\).

Entonces, podemos calcular el error de \(A\) como la raíz de la varianza.

A_optimo = p_opt[0]
A_error = p_cov[0, 0] ** 0.5

A_optimo, A_error

(2.9791178354896406, 0.15326622133629833)

El valor obtenido no da exactamente 3, pero el intervalo A_optimo ± A_error es compatible con \(A=3\).

Graficar el ajuste

Para graficar el ajuste, podemos usar la misma función que le pasamos a curve_fit. La evaluamos en los datos x y el parámetro A_optimo.

Para graficar los datos, se los suele graficar como puntos con barra de error.

y_pred = lineal(x, A_optimo)  # El "y" predicho a partir del ajuste

plt.errorbar(x, y_medido, yerr=y_error, fmt="o", label="Ajuste")
plt.plot(x, y_pred, label="Mediciones")
plt.legend()

<matplotlib.legend.Legend at 0x7fe2d8331810>

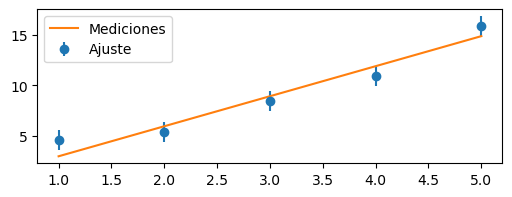
Generalmente, se acompaña este gráfico con el gráfico de los residuos.

Los residuos \(r_i\) son la diferencia entre la función \(f(x_i)\) y la medición \(y_i\) correspondiente a dicho \(x_i\): $\( r_i = y_i - f(x_i) \)$ donde se usan los parámetros óptimos para la función.

Para graficar los residuos, se suele agregar un segundo gráfico debajo, ya que comparten en eje \(x\). Es decir, \(y_i\) y \(r_i\) comparten el mismo \(x_i\).

y_pred = lineal(x, A_optimo)
residuos = y_medido - y_pred

fig, ax = plt.subplots(
    2, 1, sharex=True, figsize=(6, 6), gridspec_kw={"height_ratios": (2, 1)}
)

ax[0].errorbar(x, y_medido, yerr=y_error, fmt="o")
ax[0].plot(x, y_pred)

ax[1].errorbar(x, residuos, yerr=y_error, fmt="o")
ax[1].axhline(0, color="black")

ax[0].set(ylabel="Magnitud [unidad]")
ax[1].set(ylabel="Residuos [unidad]", xlabel="Otra magnitud [otra unidad]")

[Text(0, 0.5, 'Residuos [unidad]'),
 Text(0.5, 0, 'Otra magnitud [otra unidad]')]

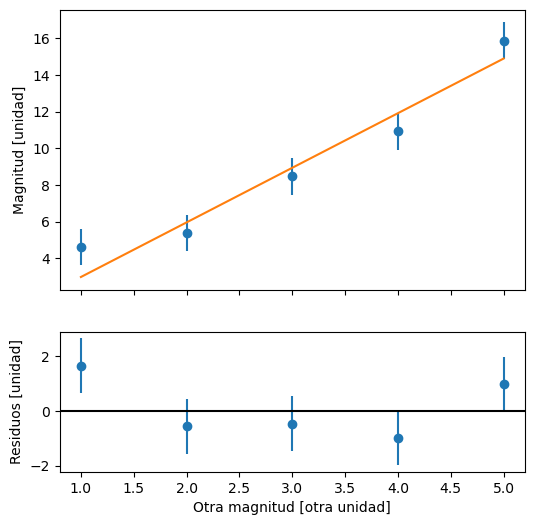
Los residuos tienen la misma unidad que el eje \(y\), y el residuo \(r_i\) tiene el mismo error que la medición \(y_i\).

Los residuos nos permiten hacer un «zoom» a la diferencia entre las mediciones y la curva teórica.

Ejercicio 1

Usando el siguiente conjunto de datos:

y = np.array([11.5, 10.2, 10.4,  9.1,  8. ,  9.7, 10.2, 11.2, 11.2,  9.6])

ajustar por cuadrados mínimos una función constante, es decir, \(f(x) = A\).

Comparar el resultado contra el promedio \(\bar{x}\) y el error del promedio \(\sigma_{\bar{x}}\).

Nota

Para x, no debería importar los valores que se usan, mientras sea del mismo largo que y.

# Escriba aquí su solución

Solución

Show code cell content Hide code cell content

y = np.array([11.5, 10.2, 10.4, 9.1, 8.0, 9.7, 10.2, 11.2, 11.2, 9.6])
x = np.arange(y.size)


def constante(x, A):
    return A


p_opt, p_cov = curve_fit(constante, x, y)

A_opt = p_opt[0]
A_error = p_cov[0, 0] ** 0.5

promedio = np.mean(y)
error_promedio = np.std(y, ddof=1) / np.size(y) ** 0.5
# ddof=1 es para que divida por N-1 al calcular la desviación estándar

print("                 A = ", A_opt)
print("          promedio = ", promedio)
print("        error de A = ", A_error)
print("error del promedio = ", error_promedio)

                 A =  10.110000000019873
          promedio =  10.11
        error de A =  0.33844415214514456
error del promedio =  0.3384441526226217

Errores diferentes en y

Por defecto, curve_fit asume que los errores en y son iguales. Pero, si cada y tiene un error distinto, podemos tenerlo en cuenta, para que le dé mayor peso a las mediciones con menor error.

Por ejemplo, en los siguientes datos, las mediciones para x=3 y x=4 tienen 10 veces más incerteza que las mediciones para x=1 y x=2:

np.random.seed(42)
x = np.array([1, 2, 3, 4])
y_error = np.array([1, 1, 10, 10])
y = 3 * x
y = np.random.normal(y, scale=y_error)

plt.errorbar(x, y, yerr=y_error, fmt="o")

<ErrorbarContainer object of 3 artists>

Para pasarle los errores a curve_fit, hay que pasarle un array (del mismo tamaño que ydata) en el parámetro sigma:

p_opt, p_cov = curve_fit(lineal, x, y, sigma=y_error)

A_opt = p_opt[0]
A_err = p_cov[0, 0] ** 0.5

plt.errorbar(x, y, yerr=y_error, fmt="o", label="Mediciones")
plt.plot(x, lineal(x, A_opt), label="Ajuste")
plt.legend()

A_opt, A_err

(3.1949912491950037, 0.4220395679483022)

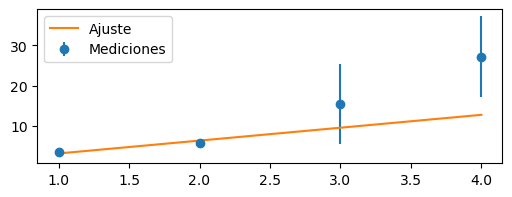
Si no los tenemos en cuenta, el valor que se obtiene es distinto:

p_opt, p_cov = curve_fit(lineal, x, y)

A_opt = p_opt[0]
A_err = p_cov[0, 0] ** 0.5

plt.errorbar(x, y, yerr=y_error, fmt="o", label="Mediciones")
plt.plot(x, lineal(x, A_opt), label="Ajuste")
plt.legend()

A_opt, A_err

(5.685734531667022, 0.8012683123310548)

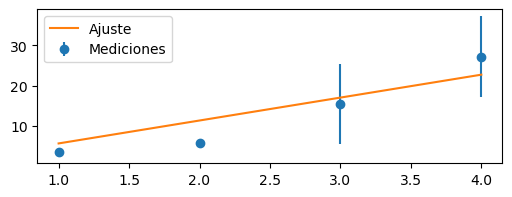
Al especificar las incertezas, curve_fit «priorizó» pasar más cerca de los puntos con menor error, resultando en una pendiente \(A\) distinta.

Múltiples parámetros

def recta(t, A, B):
    return A * t + B


x = np.linspace(0, 100, 10)
y = 3 * x + 20
y = np.random.normal(y)

p_opt, p_cov = curve_fit(recta, x, y)
p_err = np.sqrt(np.diag(p_cov))  # la raíz de la diagonal

p_opt, p_err

(array([ 2.98653563, 20.60831635]), array([0.00855936, 0.50771664]))

Los parámetros están en el mismo orden que en la definición de la función (recta):

A = p_opt[0]
B = p_opt[1]

Truco

Para evaluar la función, pueden usar recta(x, *p_opt). Es equivalente a recta(x, p_opt[0], p_opt[1]), o, en general, recta(x, p_opt[0], p_opt[1], ..., p_opt[n]).

Funciones no lineales

Para usar cuadrados mínimos con funciones no lineales, hay que darle una ayuda al algoritmo, diciendode un punto inicial para que encuentre la solución.

Una función es lineal para cuadrados mínimos si sus derivadas respecto de los parámetros no dependen de los parámetros. Por ejemplo:

\[ f(x, A, B) = A \sin(x) + B \cos(x) \]

es lineal, ya que

\[\begin{split} \begin{cases} \frac{\partial f}{\partial A} = \sin(x) \\ \\ \frac{\partial f}{\partial B} = \cos(x) \end{cases} \end{split}\]

En cambio,

\[ f(x, A, w) = A \sin(w x) \]

pero no es lineal, ya que

\[\begin{split} \begin{cases} \frac{\partial f}{\partial A} = \sin(w x) \\ \\ \frac{\partial f}{\partial w} = w A \cos(w x) \end{cases} \end{split}\]

Generemos datos para esta función no lineal, con \(A=2\) y \(w=5\), y tratemos de ajustar sin darle parámetros iniciales para la busqueda:

def func(t, A, w):
    return A * np.sin(w * t)


# Genero datos
x = np.linspace(0, 2 * np.pi, 70)
y = func(x, A=2, w=5)

# Ajusto parámetros
p, cov = curve_fit(func, x, y)

# Grafico
plt.plot(x, y, "o")
plt.plot(x, func(y, *p))

p

array([0.1409882 , 1.74692602])

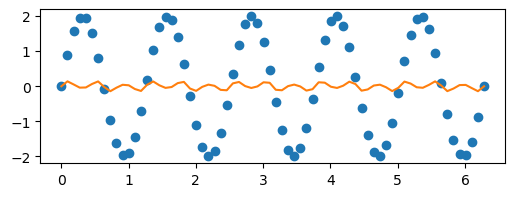
Ni hace falta ver los residuos para saber que ajustó mal.

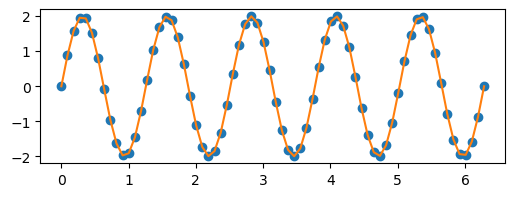
Para pasarle los parámetros iniciales, hay que usar el parámetro p0 de curve_fit:

p = (1, 5.3)
p, cov = curve_fit(func, x, y, p0=p)

plt.plot(x, y, "o")
plt.plot(x, func(x, *p))

p

array([2., 5.])

Nota

Como estos datos no tienen incerteza, los residuos son exactamente 0, y el error de los parámetros también.

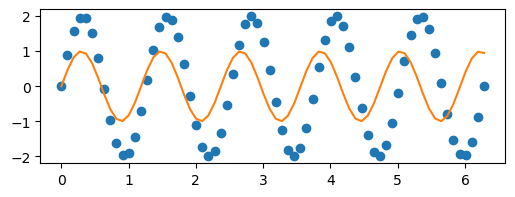
Truco

Para saber si estamos dandole parámetros iniciales razonables, podemos comentar la linea de curve_fit, y graficar la función con los parámetros iniciales p.

p = (1, 5.3)
# p, cov = curve_fit(func, x, y, p0=p)

plt.plot(x, y, "o")
plt.plot(x, func(x, *p))

p

(1, 5.3)

Muchas veces se puede automatizar la elección de los parámetros iniciales.

Por ejemplo, para \(A\) podriamos usar:

(np.max(y) - np.min(y)) / 2

1.9994817696826983

y para \(w\), obtener una estimación a través de la distancia entre máximos. Los máximos se podrían encontrar con scipy.signal.find_peaks.

Extra: bondad de ajuste

Gráfico de residuos

Para analizar la bondad de ajuste, se puede analizar el gráfico de los residuos \(r_i\), que son la diferencia entre la medición \(y_i\) para un dado \(x_i\), y el valor predicho por el modelo \(f(x_i)\):

\[ r_i = y_i - f(x_i) \]

Debido a incertezas en la medición, esperamos que \(y_i\) no sea exactamente igual al valor real. Si la función \(f\) es el modelo correcto, es decir, el que describe a nuestro experimento, esperamos que una medición \(y_i\) se «pase», para un lado o para el otro, del valor esperado \(f(x_i)\). En otras palabras, esperamos que los residuos \(r_i\) esten distribuidos alrededor de 0, de manea aleatoria.

Por ejemplo, en la siguiente figura, solo en el caso de la primer columna se observan residuos aleatorios. En la segunda columna, el modelo real es una cuadrática; en la tercer columna, son dos lineales con un «salto» en el medio.

Show code cell source Hide code cell source

def fit_and_plot(x, y, yerr, func, *, fig):
    p, _ = curve_fit(func, x, y, sigma=yerr)
    y_pred = func(x, *p)
    residuos = y - y_pred

    ax = fig.subplots(2, 1, sharex=True)
    ax[0].errorbar(x, y, yerr=yerr, fmt=".")
    ax[0].plot(x, y_pred, zorder=3)
    ax[1].errorbar(x, residuos, yerr=yerr, fmt=".")
    ax[1].axhline(0, color="black")


def recta(x, A, B):
    return A * x + B


x = np.arange(50)
yerr = np.ones_like(x)
rng = np.random.default_rng(42)

figs = plt.figure(figsize=(8, 3)).subfigures(ncols=3)

y = recta(x, A=1, B=1) + rng.normal(scale=yerr)
fit_and_plot(x, y, yerr, recta, fig=figs[0])

y = 0.008 * x**2 + x + rng.normal(scale=yerr)
fit_and_plot(x, y, yerr, recta, fig=figs[1])

y = recta(x, A=1, B=1) + rng.normal(scale=yerr)
y[x.size // 2 :] += 5
fit_and_plot(x, y, yerr, recta, fig=figs[2])

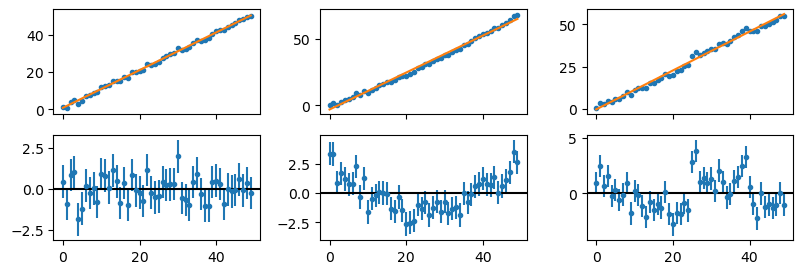
No es obvio verlo en los gráficos superiores, donde se grafican las mediciones (azul) y el modelo (naranja). Los residuos nos permiten hacer un «zoom», al considerar la diferencia entre estos.

Medidas de bondad

Hay dos medidas relacionadas a los residuos, y tratan de resumir en un número si el ajuste es bueno:

• el \(\chi^2\) (reducido)

• el coeficiente de determinación \(r^2\)

\(\chi^2\) reducido

El \(\chi^2\) reducido es un indicador para la bondad del ajuste. El \(\chi^2\) es una suma pesada de las distancias (cuadráticas) de las mediciones \(y_i\) al modelo \(f\):

\[\begin{split} \begin{align} \chi^2 &= \sum_{i=1}^N \left( \frac{y_i - f(x_i)}{\sigma_i} \right)^2 \\ &= \sum_{i=1}^N \left( \frac{r_i}{\sigma_i} \right)^2 \end{align} \end{split}\]

donde \(\sigma_i\) es el error asociado a la medición \(y_i\). Es decir, se calcula a partir de los residuos \(r_i\).

Para obtener el \(\chi^2\) reducido, dividimos por \(N-k\), donde \(N\) es la cantidad de mediciones y \(k\) la cantidad de parámetros ajustados de nuestro modelo.

\[ \chi^2_r = \frac{\chi^2}{N - k} \]

Por ejemplo, si se ajusta un modelo \(y(x) = Ax + B\), entonces \(k=2\).

def chi2_reducido(x, y, func, params, *, y_err):
    """Calcula el chi^2 reducido a partir de los datos (x, y),
    la función ajustada (`func`) y los parámetros óptimos (`params`).
    """
    n_datos = y.size
    n_params = len(params)
    y_pred = func(x, *params)
    residuos = y - y_pred
    return np.sum((residuos / y_err) ** 2) / (n_datos - n_params)

Coeficiente de determinación \(r^2\)

El coeficiente de determinación es una medida que nos da una idea de la variación en los datos que es explicada por el modelo. Mientras más cercana a \(1\), una mayor proporcion de la variación en los datos es explicada por el modelo.

En el caso de una regresión lineal, \(f(x) = Ax + B\), es igual al cuadrado del coeficiente de correlación de Pearson.

def coeficiente_de_determinacion(x, y, func, params):
    """Calcula el coeficiente de determinacion r^2 a partir de los datos (x, y),
    la función ajustada (`func`) y los parámetros óptimos (`params`).
    """
    y_pred = func(x, *params)
    residuos = y - y_pred
    return 1 - np.var(residuos) / np.var(y)

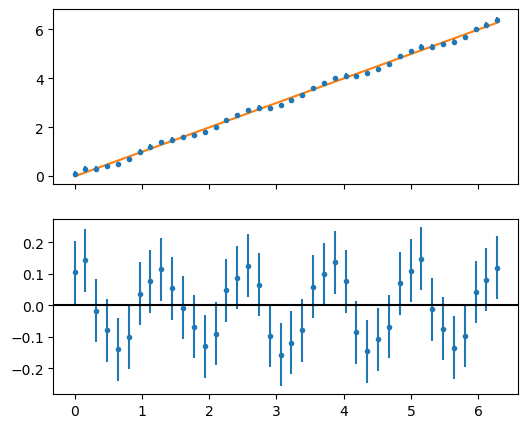
Advertencia

Calcular estos coeficientes no reemplaza a mirar los residuos.

En el siguiente ejemplo, se ve que tanto el \(\chi^2\) como \(r^2\) dan cercanos a \(1\). Pero se observa una clara estructura sinusoidal en los residuos.

Show code cell source Hide code cell source

# Simulamos las mediciones
x = np.linspace(0, 2 * np.pi, 40)
y = x + (1 / 7) * np.cos(5 * x)
# Redondeamos a un decimal para simular una medición
# con un error dado por la resolución instrumental
y_medido = np.round(y, 1)
y_error = np.full_like(y, 0.1)


# Ajustamos por una función lineal
# No es el modelo correcto, que tiene una parte sinusoidal
def func(x, A, B):
    return A * x + B


p, cov = curve_fit(func, x, y_medido)
y_pred = func(x, *p)
residuos = y_medido - y_pred

# Graficamos con los residuos
fig, ax = plt.subplots(2, 1, sharex=True, figsize=(6, 5))

ax[0].errorbar(x, y_medido, yerr=y_error, fmt=".")
ax[0].plot(x, y_pred)

ax[1].errorbar(x, residuos, yerr=y_error, fmt=".")
ax[1].axhline(0, color="black")

# Calculamos los coeficientes de bondad de ajuste
print("Chi^2 reducido:", chi2_reducido(x, y_medido, func, p, y_err=y_error))
print("           R^2:", coeficiente_de_determinacion(x, y_medido, func, p))

Chi^2 reducido: 1.0075861558210721
           R^2: 0.9972409570310523