Array (parte 2)

Array (parte 2)#

import matplotlib.pyplot as plt
import numpy as np

plt.rc("figure", dpi=100)  # aumenta la resolución de las figuras

Cargando un archivo#

Hay muchos formatos para guardar datos en archivos. El más simple es guardarlos en un archivo de texto.

En este caso, tenemos preparado un archivo de ejemplo que pueden descargar de aqui.

Si están corriendo este notebook en Google Colab, pueden descargar el archivo de ejemplo corriendo la siguiente linea en una celda de código:

!wget https://github.com/maurosilber/python-tutorial/raw/main/book/numpy/datos.txt

También, pueden descargarlo manualmente, y subirlo a Google Colab.

Si abren el archivo datos.txt en un editor de texto, como el bloc de notas o notepad, pueden ver que es un archivo de texto con un número en cada línea:

10.50
9.86
10.65
...

Para cargarlo a un array de NumPy, podemos usar la función np.loadtxt, a la que le tenemos que pasar el nombre o ubicación del archivo:

datos = np.loadtxt("datos.txt")

datos

array([10.5 ,  9.86, 10.65, 11.52,  9.77,  9.77, 11.58, 10.77,  9.53,
       10.54,  9.54,  9.53, 10.24,  8.09,  8.28,  9.44,  8.99, 10.31,
        9.09,  8.59, 11.47,  9.77, 10.07,  8.58,  9.46, 10.11,  8.85,
       10.38,  9.4 ,  9.71,  9.4 , 11.85,  9.99,  8.94, 10.82,  8.78,
       10.21,  8.04,  8.67, 10.2 , 10.74, 10.17, 15.  ,  9.7 ,  8.52,
        9.28,  9.54, 11.06, 10.34,  8.24, 10.32,  9.61,  9.32, 10.61,
       11.03, 10.93,  9.16,  9.69, 10.33, 10.98,  9.52,  9.81,  8.89,
        8.8 , 10.81, 11.36,  9.93, 11.  , 10.36,  9.35, 10.36, 11.54,
        9.96, 11.56,  7.38, 10.82, 10.09,  9.7 , 10.09,  8.01,  9.78,
       10.36, 11.48,  9.48,  9.19,  9.5 , 10.92, 10.33,  9.47, 10.51,
       10.1 , 10.97,  9.3 ,  9.67,  9.61,  8.54, 10.3 , 10.26, 10.01,
        9.77])

Si tienen problemas al cargar el archivo, puede deberse a que no se encuentre en la misma carpeta en la que están ejecutando el notebook.

Números con coma decimal#

Un problema típico es que los programas de adquisición de datos hayan guardado los números con coma, en lugar de punto, como separador decimal.

En ese caso, necesitan definir una función para convertir los números con coma, y pasársela a np.loadtxt en el parámetro converters:

def comma_to_float(x):
    x = x.decode().replace(",", ".")
    return float(x)


np.loadtxt("datos.txt", converters=comma_to_float)

En versiones de NumPy anteriores a la 1.23, hay que pasar un diccionario con numero_de_columna: funcion. En este caso, que solo hay una columna, sería para la columna 0:

np.loadtxt("datos.txt", converters={0: comma_to_float})

Comentarios o títulos#

Otro problema sucede cuando en la(s) primera(s) línea(s) del archivo no hay números, sino texto con comentarios o títulos sobre los datos. Podemos decirle que se saltee la primera linea con:

np.loadtxt("datos.txt", skiprows=1)

Si lo llegaran a necesitar, pueden ver más opciones para np.loadtxt en la documentación.

Visualizando datos#

Lo primero y más importante que hay que hacer al trabajar con datos es visualizarlos.

Una forma es usar la función plt.plot, que usamos en la sección anterior:

plt.plot(datos, marker="o")

[<matplotlib.lines.Line2D at 0x7f9f284dcbb0>]
../_images/00e2e310f50dab0f19c9cb111239975298ca6865cf3ccbdcb031b80a0651394a.png

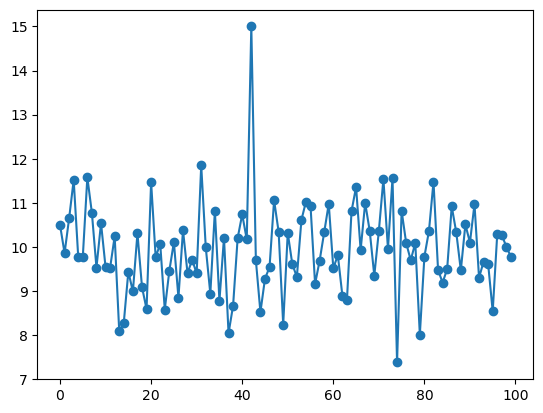
Cuando solo le pasamos un array a plt.plot, lo usa para los valores en y, mientras que para x usa la posición (o índice) de cada valor.

Es decir, x = np.arange(len(y)).

Otra forma de visualizarlos es hacer un histograma:

plt.hist(datos, bins="auto")

plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')
../_images/5a0c2669218e3fb36c1bbdf5acb9d16d08e60c475385368332e9f03f10db32a1.png

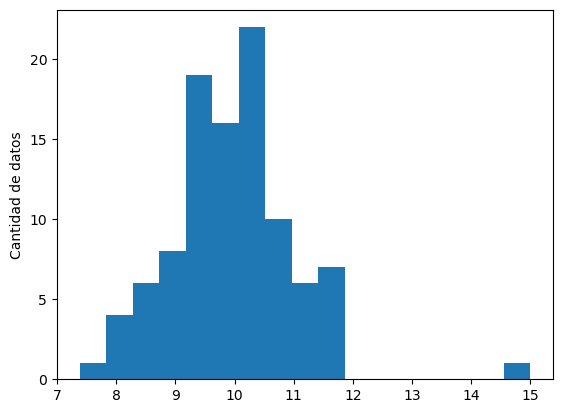
Un histograma se construye dividiendo el rango de los datos en «canastas», o bins, y contando cuantos datos caen en cada canasta.

En el histograma anterior, dejamos que la cantidad y ancho de los bins se elijan automáticamente, pero se pueden especificar manualmente.

A diferencia del gráfico de linea, en el histograma se puede entender mejor la distribución de los datos. Hay una mayor cantidad de datos alrededor de ~10, y disminuye su cantidad a medida que nos alejamos.

En ambos gráficos, podemos notar que hay un valor, alrededor de 15, que se aleja significativamente del resto. Veamos como podemos hacer para descartarlo*.

(*no vamos a discutir acá si está bien o no descartarlo)

Indexing y slicing#

Los arrays de NumPy permiten seleccionar un subconjunto de elementos de diversas maneras.

Para el siguiente array:

x = np.array([10, 20, 5, 7, 8])

podemos seleccionar un elemento particular por su índice, por ejemplo, el tercer elemento como:

x[2]

5

(recuerden que el primer elemento es el 0).

Si queremos acceder al último elemento, necesitamos saber el largo del array. Podemos usar la función len, y restarle 1:

x[len(x) - 1]

8

Python nos permite ahorrarnos el len(x) y directamente poner -1:

x[-1]

8

Para seleccionar un rango (o slice) de elementos, usamos:

x[1:3]

array([20,  5])

donde la sintaxis es x[start:stop], incluyendo start y excluyendo stop, al igual que la función range.

Otras variantes de slicing son:

  • especificar el paso con x[start:stop:step],

  • omitir start, x[:stop], donde el valor por defecto es 0,

  • omitir stop, x[start:], donde el valor por defecto es «hasta el final».

Por ejemplo, para seleccionar los dos primeros elementos:

x[:2]

array([10, 20])

Todo esto también es válido para las listas, pero lo siguiente no.

Advanced indexing#

NumPy permite indexar los arrays de otras maneras, que no son válidas para la lista.

Una de ellas es pasarle una lista con los índices de los valores que queremos:

x[[0, 1, 3]]

array([10, 20,  7])

Otra es pasarle un array de valores booleanos, es decir, True o False.

Si este array tiene True en la posición i-ésima, es que queremos quedarnos con el valor en la posición i-ésima, y False, que no lo queremos.

Para generar este array, podemos usar operadores de comparación:

x > 7

array([ True,  True, False, False,  True])

Recuerden que x era:

x

array([10, 20,  5,  7,  8])

Entonces, podemos usar ese array para quedarnos con los valores mayores a 7:

x[x > 7]

array([10, 20,  8])

Si queremos obtener los índices donde se cumple la condición, podemos usar la función np.nonzero:

np.nonzero(x > 7)

(array([0, 1, 4]),)

Ejercicio 1#

Filtrar los datos para descartar el dato cuyo valor es ~15, y rehacer el histograma para los datos filtrados.

# Escriba aquí su solución

Solución#

Hide code cell content 
datos_filtrados = datos[datos < 14]

plt.hist(datos_filtrados, bins="auto")

(array([ 1.,  4.,  6.,  8., 19., 16., 21., 11.,  6.,  7.]),
 array([ 7.38 ,  7.827,  8.274,  8.721,  9.168,  9.615, 10.062, 10.509,
        10.956, 11.403, 11.85 ]),
 <BarContainer object of 10 artists>)
../_images/3fa57c0d52c53a7e575755e7e035159029278350cede51e6d521d3ee998b9821.png

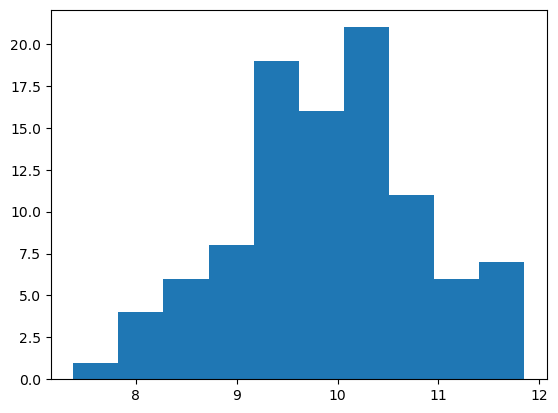
Reducción#

De esta parte sobre los arrays de NumPy, nos queda aprender las operaciones de reducción.

Hasta ahora, habíamos visto las operaciones elemento a elemento y de broadcasting.

En la primera, a partir de dos arrays iguales, se generaba un tercero del mismo tamaño.

En la de broadcasting, al combinar un número con un array, el número se «estiraba» al tamaño del array, y se combinaba elemento a elemento.

En las operaciones de reducción, partimos de un array y lo reducimos a un número.

Por ejemplo, para este array:

x = np.array([1, 2, 4, 3])

podemos usar la función np.sum para calcular la suma:

np.sum(x)

10

o np.max para calcular el máximo:

np.max(x)

4

o np.argmax para encontrar la posición del máximo:

np.argmax(x)

2

y muchas otras que pueden buscar en la documentación.

Nota

Puede parecer innecesario que haya un término específico, reducción, para operaciones como calcular la suma o el máximo. Pero va a tener sentido cuando veamos arrays en 2 o más dimensiones.

Ejercicio 2#

Para el array de datos filtrados, calcular la cantidad de datos, su promedio \(\bar{x}\), y su desviación estándar \(\hat{\sigma}\).

La fórmula para estos últimos es:

\[\begin{split} \begin{align} \bar{x} &= \frac{x_1 + \ldots + x_n}{n} &&= \frac{1}{n} \sum_{i=1}^n x_i \\ \\ \hat{\sigma} &= \sqrt{\frac{(x_1 - \bar{x})^2 + \ldots + (x_n - \bar{x})^2}{n}} &&= \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2} \end{align} \end{split}\]

Ayuda: usar las funciones np.size, np.sum. Para restar el promedio a todos los números, rever la sección, broadcasting.

# Escriba aquí su código

Solución#

Hide code cell content 
x = datos_filtrados

total = np.size(x)
promedio = np.sum(x) / total
varianza = np.sum((x - promedio) ** 2) / total
desv_estandar = varianza**0.5

total, promedio, desv_estandar

(99, 9.896464646464647, 0.9080919202475125)

Si necesitáramos calcular constantemente la desviación estándar de los datos, nos convendría definir una función que encapsule esas operaciones.

Pero esas funciones ya están definidas en NumPy:

np.size(x), np.mean(x), np.std(x)

(99, 9.896464646464647, 0.9080919202475125)

  • mean es media o promedio en inglés,

  • std viene de standard deviation, desviación estándar en inglés.

Contenido