Múltiples mediciones#
Al realizar múltiples mediciones, podemos mejorar la precisión de la magnitud que estamos midiendo. Hay varias formas de realizar múltiples mediciones, de las cuales consideraremos 3 casos.
Imaginen que tenemos \(N=10\) objetos idénticos, que vamos a representar con un rectángulo, y queremos medir su longitud.

Vamos a asumir que son exactamente iguales, es decir, si tuviésemos infinita precisión para medir, mediríamos lo mismo para todos.
Estos objetos no representan necesariamente rectángulos físicos, sino que pueden representar intervalos de tiempo.
Caso 1: mediciones independientes#
Una primera opción es medirlos de forma independiente:
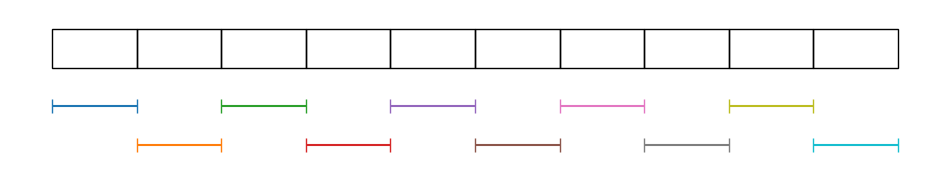
En ese caso, tenemos dos posibilidades, según si estamos limitados por la resolución instrumental o no.
Con error por resolución instrumental#
Si el error está dado por la resolución \(\Delta L\) de nuestro instrumento, vamos a medir siempre lo mismo. Hacer más mediciones no aporta nada. En este caso, el error será:
Con error estadístico#
En cambio, si en cada medición tenemos un error estadístico \(\sigma_L\), podemos promediar las mediciones y disminuir el error. El error del promedio \(\langle L \rangle\) disminuye como
El error \(\sigma_{\langle L \rangle}\) de este promedio \(\langle L \rangle\) no depende de la resolución instrumental \(\Delta L\), si \(\sigma_L \gtrsim \Delta L\). Pero no significa que podamos hacerlo tan chico como queramos, ya que sí depende de la calibración instrumental. Por ejemplo, un cronómetro típico tiene una resolución instrumental de \(10 \text{ ms} = 0.01 \text{ s} = 10^{-2} \text{ s}\), pero tiene un error de calibración del orden de \(\sim 5 \text{ μs} = 5 \times 10^{-6} \text{ s}\). Midiendo intervalos de tiempo a mano, donde se tiene un error del orden de \(\sigma_T \approx 50 \text{ ms}\), hay que tener cuidado de no promediar más de \(N = \left(\frac{50 \text{ ms}}{5 \text{ μs}}\right)^2 = 10^8\) veces.
Advertencia
Probablemente se rompan otras hipótesis de la teoría antes de llegar a ese nivel de precisión. Por ejemplo, en el caso del péndulo, la aproximación de pequeñas oscilaciones.
Caso 2: midiendo extremos#
Si alineamos los \(N\) objetos, podemos calcular indirectamente el largo \(L_1\) de un objeto a partir del largo \(L_N\) de \(N\) objetos consecutivos.
<ErrorbarContainer object of 3 artists>

Supongamos que el error de medir directamente \(L_1\), es igual al de medir directamente \(L_N\):
Entonces, por propagación de errores, medir indirectamente \(L_1\) es:
que disminuye más rápido que el promedio.
Repitiendo la cuenta anterior, al medir a mano con un cronómetro, si \(N = \left(\frac{50 \text{ ms}}{5 \text{ μs}}\right)^1 = 10^4 = 10.000\), tendríamos que tener en cuenta el error de calibración.
Ejemplo del caso 2#
Imaginemos que la sección mide \(L_1^{real} = 10.12 \text{ mm}\), pero medimos con una regla de resolución \(1 \text{ mm}\). Si medimos una única sección, nuestra medición va ser \(L_1^{medido} = (10 \pm 1) \text{ mm}\). Pero, si medimos \(N=10\) secciones consecutivas, cuyo largo es
vamos a medir \(L_{10}^{medido} = 101 \pm 1 \text{ mm}\). Noten que es diferente a multiplicar por \(N=10\) la medición de una sección:
Calculando indirectamente \(L_1\), y propagando, llegamos a:
que tiene un error 10 veces menor que la medición directa de \(L_1\). ¡Ganamos un decimal!
Caso 3: mediciones consecutivas#
En el caso 3, al igual que el caso 2, alineamos todos los objetos para medirlos. Pero, medimos todas las distancias intermedios \(L(n)\):

¿Cómo calculamos el largo \(L_1\) de un segmento a partir de estas mediciones?
Opción 1 (incorrecta)#
Podemos tomar las diferencias entre puntos consecutivos:
y promediarlas.
¿Si hacemos un promedio, el error no debería disminuir como \(1 / \sqrt{N}\)? En ese caso, ¿no es mejor el caso anterior, donde solo mediamos los extremos y el error disminuía como \(1 / N\)?
Como los \(\Delta L_n\) no son independientes, no se cumplen las hipótesis para que el error del promedio sea \(\sigma_L / \sqrt{N}\).
Si escribimos explícitamente los \(\Delta L_n\):
vemos que \(\Delta L_1\) y \(\Delta L_1\) comparten la medición \(L(1)\). Si hacemos un promedio de estos:
quedan solo los extremos \(L(2)\) y \(L(0)\).
Si lo extendemos a las \(N\) mediciones,
llegamos a lo mismo que calculábamos en el caso anterior.
Opción 2#
Para combinar las mediciones \(L(n)\), aprovechando la información de las mediciones intermedias, y obtener \(L_1\), se puede realizar un ajuste lineal:
donde \(n\) es la cantidad de secciones consecutivas.
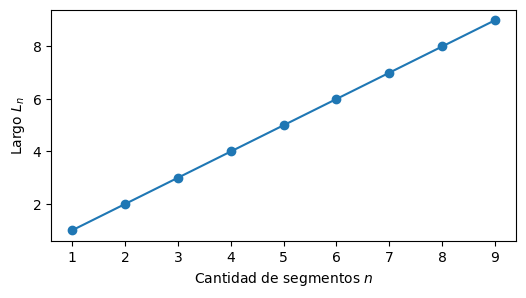
En este caso, el error de \(L_1\) disminuye aún más rápido que en el caso anterior. Según Bevington and Robinson[1], ecuaciones (6.23) y (6.13):
Dado que \(n = \{1, \ldots, N\}\),
Reemplazando en la ecuación anterior:
Repitiendo la cuenta para el cronómetro, si \(N \approx 500\), tendríamos que tener en cuenta el error de calibración. Ya no es (tan) inalcanzable.
Aclaración importante#
Hay un detalle importante, que lo diferencia de simplemente repetir \(N\) veces el caso 2, una vez para cada \(L(n)\):
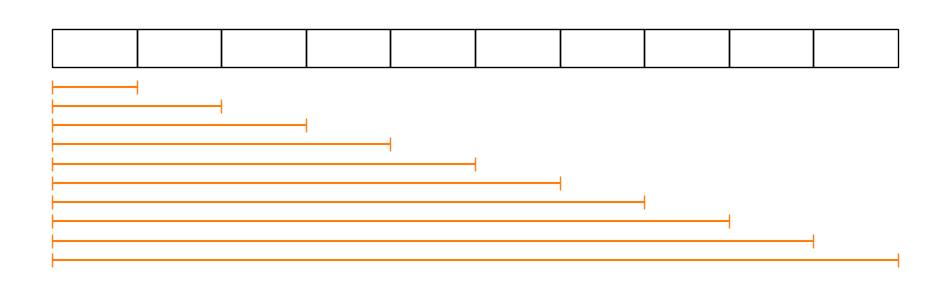
En el caso 3, las mediciones comparten el mismo origen, mientras que en el esquema anterior, estamos volviendo a medir el origen.
Es más claro con un ejemplo. Para mediciones con una regla, se puede:
apoyar la regla una vez y tomar todas las mediciones intermedias
apoyar la regla \(N\) veces, y tomar cada vez un \(L(n)\) distinto.
En este último caso, cada vez que apoyamos la regla, estamos introduciendo un error en el origen.

