Promedio, desviación estándar y error del promedio#
En esta sección, vamos a presentar dos medidas para resumir un conjunto de mediciones:
el promedio, que es una medida de centralidad,
la desviación estándar, que es una medida de dispersión.
También vamos a presentar el error del promedio, y discutir cuando usarlo para reportar el resultado de nuestras mediciones.
Show code cell content
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(42)
plt.rc("figure", dpi=100, figsize=(6, 3))
Generando datos aleatorios#
Para usar de ejemplo, vamos generar muchos datos con distribución normal:
rng = np.random.default_rng()
data = rng.normal(loc=10, scale=1, size=100_000)
Podemos ver algunos de los primeros valores:
data[:5]
array([ 9.32258899, 10.62875006, 10.68482129, 11.92361973, 9.60848788])
Pero es mejor visualizarlos gráficamente.
Si hacemos un histograma, vemos que estos están distribuidos alrededor de un valor central:
plt.hist(data, bins="auto")
plt.ylabel("Cantidad de datos")
Text(0, 0.5, 'Cantidad de datos')
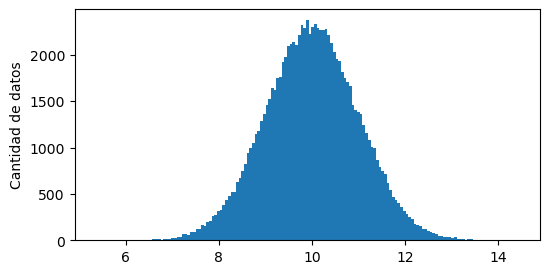
¿Cómo podemos resumir estos datos?
Una forma es dar un intervalo. Equivalentemente, dar un valor para el centro de los datos, un otro para la dispersión de estos.
Medidas de dispersión#
Hay muchas medidas posibles de dispersión. Según cuál sea la distribucion de los datos, algunas son más apropiadas que otras.
Rango#
El rango de los datos es la diferencia entre el valor máximo y el mínimo:
Podemos calcularla así:
np.max(data) - np.min(data)
8.778813921305696
o, con la función np.ptp (peak to peak):
np.ptp(data)
8.778813921305696
Este valor va a depender de la cantidad de datos que consideremos. Si solo hubiesemos hecho las primeras 3 mediciones:
data[:3]
array([ 9.32258899, 10.62875006, 10.68482129])
el rango para estas mediciones es:
np.ptp(data[:3])
1.362232307322012
Veamos que sucede con esta medida en función de la cantidad de mediciones que consideramos.
En función de la cantidad de mediciones#
Cómo vamos a repetir este análisis más adelante, hagamos una función que encapsule esto:
Show code cell source
def generate_axes():
fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(8, 2))
for ax in axes:
ax.set(xlabel="N datos")
ax.grid()
axes[1].set(xscale="log")
return axes
def valor_en_funcion_de_n(data, func, *, ylabel=None, axes=None):
if axes is None:
axes = generate_axes()
if ylabel is None:
ylabel = func.__name__
n_datos = np.arange(1, data.size)
maxmin = [func(data[:i]) for i in n_datos]
for ax in axes:
ax.plot(n_datos, maxmin)
axes[0].set(ylabel=ylabel)
Entonces, calculamos el rango para los primeros \(N\) datos, y gráficamos como varía este valor en función de \(N\):
valor_en_funcion_de_n(data, func=np.ptp, ylabel="rango")
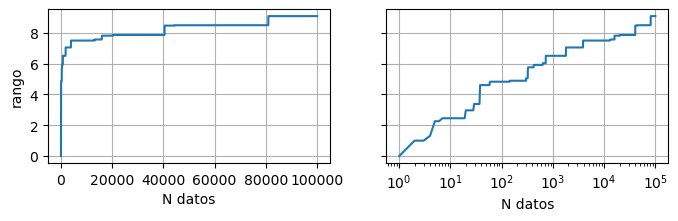
Nota
El eje \(x\) del gráfico de la derecha está en escala logarítmica. La distancia entre \(x=10\) y \(x=100\) es la misma que entre \(x=100\) y \(x=1000\).
Este valor depende de la cantidad de datos que medimos, y sigue creciendo a medida que consideramos más mediciones.
Si miramos el histograma de los datos, hay cada vez menos mediciones a medida que nos alejamos del centro. Es decir, tienen menor probabilidad de darse.
Pero, cada tanto, la siguiente medición está más lejos del resto y es la que se considera para el rango. Por eso se ven saltos en la curva en función de las mediciones.
Si repetimos esto para otros sets de datos, vemos que sucede lo mismo, pero los saltos se dan en otros lugares:
axes = generate_axes()
for _ in range(10):
valor_en_funcion_de_n(
np.random.normal(loc=10, scale=1, size=10_000),
func=np.ptp,
ylabel="max - min",
axes=axes,
)
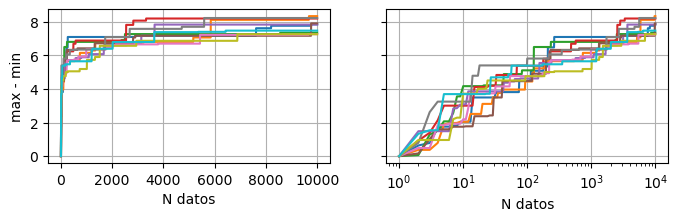
En conclusión, no es una buena medida del ancho para datos con distribución gaussiana.
Desviación estandar#
La desviación estándar \(s\) o \(\sigma\) es otra medida de dispersión de los datos. Se calcula como:
donde \(\bar{x} = \sum_{i=1}^N x_i\) es el promedio de los datos.
En Python, podemos calcularla así:
np.std(data, ddof=1) # ddof=1 es por el N-1
1.0004340213614529
¿De donde sale?#
Supongamos que conocemos el valor real \(\mu\) del centro de las mediciones. Entonces, podemos medir las distancias \(d_i\) de las mediciones \(\{x_i\}\) al valor real:
y calcular la dispersión como «un promedio» de estas distancias. Hay dos opciones:
El promedio:
El promedio de los cuadrados:
que se lo conoce como la varianza. Por ahora, vayamos con esta la segunda opción.
Como las mediciones \(\{x_i\}\) son conocidas, podemos pensar en esta expresión como una función de \(\mu\), que no conocemos:
y preguntarnos: ¿cuál es el \(\mu\) para el que esta suma es mínima?
Nota
Esta función es una cuadrática o parábola en función de \(\mu\), y tiene un valor mínimo.
Para encontrar analíticamente este valor, derivamos con respecto a \(\mu\) e igualamos a 0:
Si hacen esta cuenta, y despejan el \(\mu=\bar{x}\) óptimo, obtienen:
es decir, es el promedio de los \(\{x_i\}\).
Nota
Si lo hubiesemos hecho con la suma de las distancias, el valor que minimiza esa suma es la mediana, que es «el valor del medio» si ordenamos las mediciones de menor a mayor. Pero no se puede llegar de la misma manera, ya que el módulo no es derivable.
Como estamos estimando el valor real \(\mu\) con el promedio \(\bar{x}\), por razones estadísticas que no son muy relevantes ahora (ver Corrección de Bessel), se utiliza \(N-1\) en lugar de \(N\) en el denominador para calcular la varianza:
Finalmente, como estabamos buscando una medida del ancho de las mediciones, y la varianza tiene unidades de \(x^2\), tomamos la raíz, que se conoce como la desviación estándar.
En función de la cantidad de mediciones#
A diferencia del rango, la desviación estándar no crece indefinidamente a medida que tomtamos más mediciones:
valor_en_funcion_de_n(data, func=np.std, ylabel="Desv. estándar")
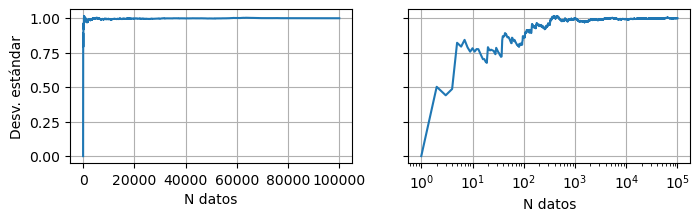
Podemos repetimos esto para nuevos sets de mediciones:
axes = generate_axes()
for _ in range(10):
valor_en_funcion_de_n(
np.random.normal(loc=10, scale=1, size=10_000),
func=np.std,
ylabel="Desv. estándar",
axes=axes,
)
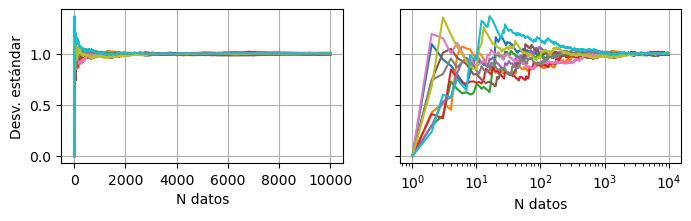
En todos los casos, la desviación estándar tiende al mismo valor: \(\sigma = 1\).
Esto es esperable ya que, cuando simulamos los datos, estamos eligiendo ese valor para el ancho de la gaussiana.
Pero la separación entre curvas es mayor cuando la cantidad de datos es menor: el error de la desviación estándar disminuye con la cantidad de datos.
Interpretación probabilística#
Al introducir la desviación estándar, estabamos buscando una medida para estimar la dispersión de las mediciones. Esta se comporta mejor que el rango, pero no cubre todas las mediciones:
plt.hist(data, bins="auto")
plt.axvline(np.mean(data), color="C1", label=r"$\bar{x}$")
plt.axvspan(
np.mean(data) - np.std(data),
np.mean(data) + np.std(data),
color="C1",
alpha=0.3,
label=r"$\bar{x} \pm \sigma$",
)
plt.legend(fontsize="x-large")
<matplotlib.legend.Legend at 0x7f3fec5a2110>
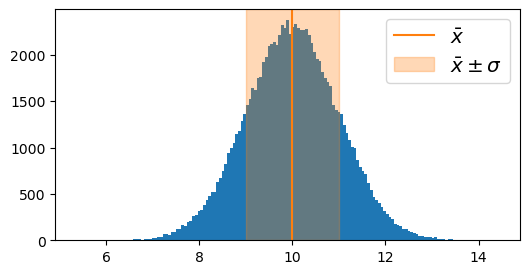
En general, la interpretación que se le da a este intervalo depende de la distribución de las mediciones.
Para una distribución gaussiana, la probabilidad \(P\) que una medición este entre \(\mu \pm k \, \sigma\) es:
k |
P |
|---|---|
1 |
0.68 |
2 |
0.95 |
3 |
0.997 |
4 |
0.99993 |
5 |
0.9999994 |
Nota
Para una versión más general de esto, pueden ver la Desigualdad de Chebyshev.
Entonces, para comparar mediciones, el intervalo \(\mu \pm \sigma\) no es estricto, a diferencia de cuando no tenemos error aleatorio.
Por ejemplo, en física de particulas, a una medición no se la considera «distinta a lo esperado» hasta que no esté más lejos de \(5 \sigma\),
Medidas de centralidad#
El promedio y su error#
Al igual que las medidas de dispersión, hay muchas medidas de centralidad. Una de ellas es el promedio \(\bar{x}\):
que es la que hace que la desviación estándar sea mínima.
En función de la cantidad de mediciones#
Al igual que antes, veamos como se comprota el promedio en función de la cantidad de mediciones:
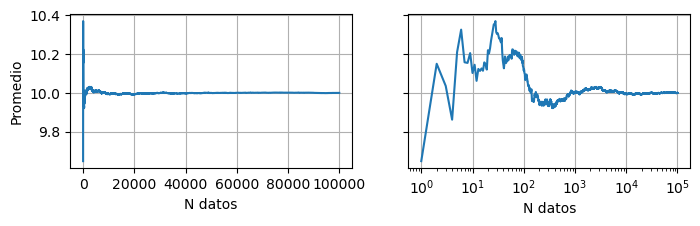
valor_en_funcion_de_n(data, func=np.mean, ylabel="Promedio")
axes = generate_axes()
for _ in range(10):
valor_en_funcion_de_n(
np.random.normal(loc=10, scale=1, size=10_000),
func=np.mean,
ylabel="Promedio",
axes=axes,
)
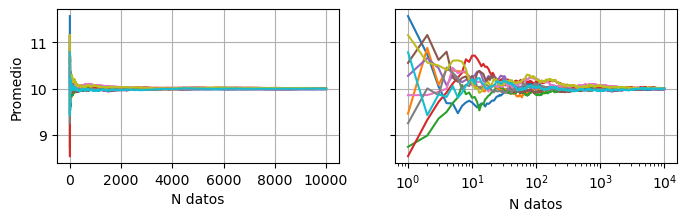
En todos los casos tiende a 10, que es el valor de \(\mu\) que elegimos para la gaussiana.
Al igual que con la desviación estándar, el promedio tiene un error \(\sigma_{\bar{x}}\), y este es menor a medida que tomamos más mediciones.
Este error lo podemos estimar como:
donde \(\sigma\) es la desviación estándar de las mediciones, y \(N\) la cantidad de mediciones que promediamos.
¿Qué reportamos?#
Supongamos que hicimos \(N\) mediciones \(\{x_i\}\), y que tienen una distribución (aproximadamente) gaussiana.
Para calcular el centro de esta distribución, podemos usar el promedio.
Para el error, tenemos dos medidas:
la desviación estándar \(\sigma\), que es el error al hacer una medición.
el error del promedio \(\sigma / \sqrt{N}\), que es el error al hacer un promedio de \(N\) mediciones.
¿Cuál de estas dos opciones usamos para reportar el resultado?
La estadística no tiene una respuesta para esto. Hay que pensar en el experimento.
Hay dos casos extremos. Si volviéramos a realizar las mediciones con un instrumento más preciso, podríamos:
no observar una dispersión (\(\sigma\)) menor
observar la misma dispersión (\(\sigma\)) que antes
Por ejemplo, si usamos una cinta métrica para medir la altura de distintas personas, vamos a obtener valores entre 150 cm y 190 cm. Esa dispersión no va a cambiar por usar un instrumento más preciso.
En cambio, si medimos la altura de una única persona, está magnitud está bien definida. Si observamos una dispersión en las mediciones, son por error de medición. Este debería disminuir si usamos un instrumento o método más preciso.
En este segundo caso, queremos reportar el promedio con el error del promedio:
que es el intervalo que podría medir otra persona con un método y/o instrumento más preciso.
En cambio, en el primer caso, no es tan relevante saber el error del promedio. Si tomaramos una nueva persona para medir su altura, esperamos que este en:
sin importar que tan preciso sea nuestro instrumento.
Nota
En la práctica, podemos tener una combinación de ambos efectos. Por ejemplo, si medimos una única persona, esta puede cambiar la forma en que se para entre mediciones y, por lo tanto, «cambiar su altura».