Photogate explicado paso a paso

Photogate y MotionDAQ

El photogate, o fotosensor de barrera, es un sensor que permite medir tiempos de manera muy precisa. Para ello, tiene un emisor de luz infrarroja y un detector de luz. Cuando detecta la luz infrarroja, emite una señal de un dado voltaje. Cuando un objeto atravieza el sensor, bloquea la luz, y el sensor emite otro voltaje. Midiendo el tiempo cuando se produce el cambio de voltaje, podemos saber cuando un objeto pasó por el photogate.

La señal del photogate la podemos digitalizar con el MotionDAQ. Este mide el voltaje que emite el sensor para un conjunto de tiempos discretos. El tiempo \(\Delta t\) entre mediciones se puede controlar, elijiendo la frecuencia de muestreo \(f = 1/\Delta t\). Luego, podemos exportar estas mediciones como un archivo de texto.

En este notebook, vamos a ver como podemos cargar y analizar esas mediciones para obtener los tiempos en que se bloqueó o desbloquó el sensor.

Paquetes

Importamos los paquetes y funciones que vamos a necesitar:

• la función Path de pathlib, que nos permite manejar las «rutas» o ubicaciones de los archivos. En particular, la vamos a usar para encontrar todos los archivos de medición que usemos.

• numpy, para operar con arrays numéricos

• matplotlib, para graficar

• pandas, que solo vamos a usar para leer los archivos. Es muy usado porque proporciona varias comodidades sobre numpy, pero es confuso de usar al principio.

from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

Buscando los archivos

Buscamos todos los archivos que terminan con .txt en la carpeta actual.

Nota

Pueden decargar unos archivos de muestra de acá:

• 1cm.txt

• 2cm.txt

carpeta = Path()  # carpeta actual
archivos = list(carpeta.glob("*.txt"))  # lista de archivos que terminan con .txt

archivos

[PosixPath('2cm.txt'), PosixPath('1cm.txt')]

Cargando datos de un archivo

Si abrimos un archivo en un editor de texto (notepad), veriamos lo siguiente:

!head "1cm.txt"

date/time: ,14/03/2023,11:02 a.m.

Run 1



time	(V)

0,000000	3,008515E-1

0,005000	3,083884E-1

0,010000	3,033638E-1

0,015000	3,083884E-1

0,020000	3,134130E-1

0,025000	3,134130E-1

Es un archivo de texto, donde las primeras dos filas tienen metadata:

• la hora a la que se tomó la medición, y

• número de corrida.

Las siguientes filas tienen los datos agrupados en dos columnas, que estan separadas por «un espacio». En programación, hay al menos dos tipos de espacios:

• " ", el espacio común que inserta la barra espaciadora, y

• "\t", el espacio que inserta la tecla Tab.

En este caso, es el segundo.

También, los números usan una coma como separador decimal.

Todo esto hay que decirselo a Python, para que sepa como interpretar el archivo.

df = pd.read_csv(
    archivos[0],  # el primer archivo,
    skiprows=3,  # que ignore las primeras 3 filas
    delimiter="\t",  # separador Tab
    decimal=",",  # coma decimal
)

df

	time	(V)
0	0.000	0.300851
1	0.005	0.308388
2	0.010	0.303364
3	0.015	0.308388
4	0.020	0.313413
...	...	...
991	4.955	0.303364
992	4.960	0.303364
993	4.965	0.303364
994	4.970	0.313413
995	4.975	0.303364

996 rows × 2 columns

La variable df tiene un DataFrame de pandas. Podemos extraer el array de numpy interno con df.values:

data = df.values

data

array([[0.       , 0.3008515],
       [0.005    , 0.3083884],
       [0.01     , 0.3033638],
       ...,
       [4.965    , 0.3033638],
       [4.97     , 0.313413 ],
       [4.975    , 0.3033638]])

Este array tiene 996 filas y 2 columnas:

data.shape

(996, 2)

Para más (o menos) comodidad, podemos separar cada una en una variable:

t = data[:, 0]  # tiempo [s]
v = data[:, 1]  # voltaje [V]

Graficar los datos

Es importante visualizar los datos, para asegurarnos de que no haya habido problemas de medición. Grafiquemos estas dos variables:

plt.figure(figsize=(6, 2))
plt.xlabel("Tiempo [s]")
plt.ylabel("Voltaje [V]")
plt.plot(t, v)

[<matplotlib.lines.Line2D at 0x7f42ae9443d0>]

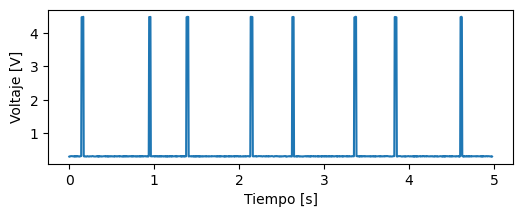
Hagamos zoom sobre el primer salto, y graficamos los valores discretos de la señal:

plt.figure(figsize=(6, 2))
plt.xlabel("Tiempo [s]")
plt.ylabel("Voltaje [V]")
plt.plot(t, v, marker="o", linestyle="--")
plt.xlim(0.12, 0.18)
plt.grid()

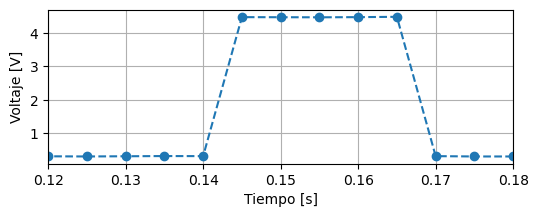
Preguntas

• ¿En qué tiempo se bloqueó el sensor?

• ¿Qué error podemos asignarle a ese tiempo?

• ¿Cómo podemos encontar «automaticamente» ese tiempo? ¿Qué distingue a esos tiempos de los demás?

Calcular diferencias de voltaje

Para encontrar el cambio de voltaje, podemos calcular la diferencia entre un punto \(i\) y el siguiente \(i+1\). numpy incluye una función para esto: np.diff.

dif_de_v = np.diff(v)

Este vector tiene un valor menos el original, ya que no puede calcular la diferencia del último con el siguiente (¡ya no hay siguiente!).

np.size(v)

996

np.size(dif_de_v)

995

Para graficarlo, vamos a ignorar el tiempo, y dejar que grafique contra el número de indice del array:

plt.figure(figsize=(6, 2))
plt.xlabel("Indice del array")
plt.ylabel("Dif. de voltaje [V]")
plt.plot(dif_de_v, marker=".", linestyle="--")

[<matplotlib.lines.Line2D at 0x7f42cc805e70>]

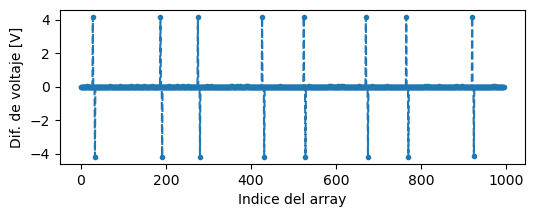
Si hacemos zoom al primer salto, y superponemos la señal original, podemos ver que da (practicamente) 0 en todos lados, menos en los cambios de voltaje:

plt.figure(figsize=(6, 2))
plt.xlabel("Indice del array")
plt.ylabel("Voltaje [V]")
plt.plot(v, label="Voltaje", marker=".", linestyle="--")
plt.plot(dif_de_v, label="Dif. de voltaje", marker=".", linestyle="--")
plt.legend()
plt.xlim(0, 40)

(0.0, 40.0)

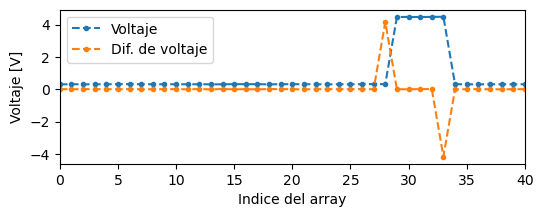
Pero ojo, no es exactamente 0, ya que el voltaje fluctua levemente:

v[:5]

array([0.3008515, 0.3083884, 0.3033638, 0.3083884, 0.313413 ])

dif_de_v[:5]

array([ 0.0075369, -0.0050246,  0.0050246,  0.0050246,  0.       ])

Encontrar valores que cumplen cierta condicion

Para encontrar los valores dentro de un array que cumplen cierta condicion, se pueden hacer lo siguiente:

y = np.array([0, 0, 5, 5, 0, 5])  # array de ejemplo

y > 3

array([False, False,  True,  True, False,  True])

que devuelve un vector de verdaderos (True) y falsos (False) para cada elemento.

Si quieren obtener las posiciones o indices donde se cumplió la condición, es decir, donde están los True, pueden hacer así:

pos = np.nonzero(y > 3)

pos

(array([2, 3, 5]),)

Si quisieran extraer los valores de y que están en esas posiciones:

y[pos]

array([5, 5, 5])

Entonces, en el caso de la señal del fotosesnsor, podemos encontrar los «saltos», tanto positivos y negativos, como:

pos = np.nonzero(np.abs(dif_de_v) > 2.5)

pos

(array([ 28,  33, 187, 191, 275, 280, 426, 431, 524, 528, 670, 675, 765,
        770, 920, 924]),)

Peor no nos interesa obtener el valor del voltaje en esas posiciones, sino los tiempos en esas posiciones:

tiempo_saltos = t[pos]

tiempo_saltos

array([0.14 , 0.165, 0.935, 0.955, 1.375, 1.4  , 2.13 , 2.155, 2.62 ,
       2.64 , 3.35 , 3.375, 3.825, 3.85 , 4.6  , 4.62 ])

Encontrar periodos

Finalmente, si nos interesa encontrar periodos, podemos calcular las diferencias entre los tiempos correspondientes. Esto dependerá del experimento.

Por ejemplo, si necesitamos obtener 1 de cada 4 tiempos, podemos tomar una «rebanada» (slice) del array con la siguiente expresion:

tiempo_saltos[::4]

array([0.14 , 1.375, 2.62 , 3.825])

En general, la notación es array[desde:hasta:paso]. Si omitimos uno, por defecto son:

• desde: 0

• hasta: hasta el final

• paso: 1

Por ejemplo:

• array[2:8:3]

• array[:5]: hasta el 5to elemento.

• array[10::3]: desde el 10mo elemento cada 3.

• etc.

Luego, podriamos calcular la diferencia entre valores consecutivos con:

np.diff(tiempo_saltos[::4])

array([1.235, 1.245, 1.205])

Más periodos

Para aprovechar todos los datos, también pueden calcular los periodos cada 4, pero empezando de la segunda medicion (indice 1):

np.diff(tiempo_saltos[1::4])

array([1.235, 1.24 , 1.21 ])

Y desde la tercera y cuarta medicion.

Pueden hacer todo esto en un paso con la siguiente expresion:

tiempo_saltos[4:] - tiempo_saltos[:-4]

array([1.235, 1.235, 1.195, 1.2  , 1.245, 1.24 , 1.22 , 1.22 , 1.205,
       1.21 , 1.25 , 1.245])

Para ver que esta haciendo, generemos un array más simple:

x = np.arange(6)
x

array([0, 1, 2, 3, 4, 5])

Si tomamos desde el segundo hasta el final, obtenemos:

x[2:]

array([2, 3, 4, 5])

Y si tomamos desde el principio hasta 2 menos del final, tenemos:

x[:-2]

array([0, 1, 2, 3])

Luego, haciendo la diferencia elemento a elemento, es hacer la diferencia cada dos elementos:

x[2:] - x[:-2]

array([2, 2, 2, 2])