Error de resolución o cuantización#
Si queremos medir un tiempo \(t\), que es una variable continua, podemos usar un cronómetro. Sin embargo, este tiene una cantidad de decimales finita, por lo que no tenemos acceso directo a esta variable continua. Es decir, si \(t = 12.3456789\ldots \text{ s}\), medimos \(\hat{t} = 12 \text{ s}\), (o \(12.3 \text{ s}\), si tenemos un cronómetro con 1 décimo de segundo de resolución). ¿Cómo nos afecta esto en la precisión con la que podemos determinar el tiempo \(t\)?
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats
Simulando una medición#
Asumamos que \(t \sim N(t_0, \sigma)\), es decir, tiene una distribución normal centrada en \(t_0\) y de ancho \(\sigma\):
t0 = 12.3456789
sigma = 1
t = scipy.stats.norm(t0, sigma)
Con esto, podemos simular una medición de la variable continua \(t\):
ti = t.rvs()
ti
np.float64(11.801885430856078)
Y para simular la medición que vemos con el cronómetro, podemos redondear este número:
ti.round()
np.float64(12.0)
donde nuestro error de resolución sería \(1\).
Simulando la distribución#
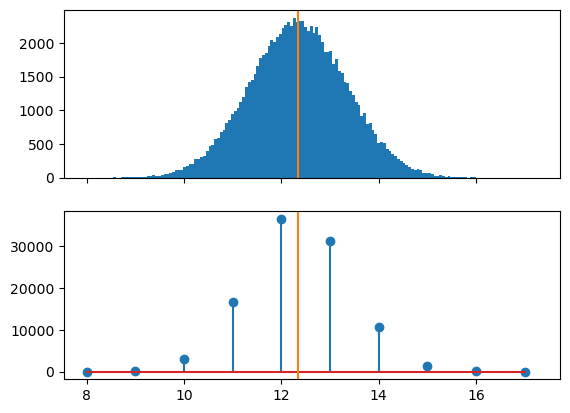
Si repetimos este proceso multiples veces, podemos simular (y graficar) la distribución de la variable continua y la redondeada:
t_continua = t.rvs(size=100_000)
t_redondeada = t_continua.round()
fig, axes = plt.subplots(2, sharex=True)
axes[0].hist(t_continua, bins="auto")
axes[1].stem(*np.unique_counts(t_redondeada))
for ax in axes:
ax.axvline(t0, color="C1")
El promedio#
Si calculamos el promedio de la variable continua, esperamos que se acerque al valor de \(t_0\):
t_continua.mean()
np.float64(12.342980702124938)
donde el error (cuanto se aleja de \(t_0\)):
t_continua.mean() - t0
np.float64(-0.0026981978750608704)
depende de la cantidad de mediciones que promediamos como:
sigma / np.sqrt(t_continua.size)
np.float64(0.003162277660168379)
(el error del promedio \(\sigma / \sqrt{N}\)).
Si promediamos la variable redondeada:
t_redondeada.mean()
np.float64(12.34308)
vemos que también se acerca a ese valor. El error es:
t_redondeada.mean() - t0
np.float64(-0.0025988999999988494)
Si comparamos directamente los promedios entre sí:
print(f"{ t_continua.mean() = }")
print(f"{t_redondeada.mean() = }")
t_continua.mean() = np.float64(12.342980702124938)
t_redondeada.mean() = np.float64(12.34308)
la diferencia recién aparece en el tercer decimal y es:
t_redondeada.mean() - t_continua.mean()
np.float64(9.929787506202103e-05)
Es decir, nos podemos acercar a la variable continua, sin redondear, con una precisión por debajo de la resolución de nuestro instrumento.
La varianza#
Para la distribución continua, esperamos que la varianza sea \(\sigma^2 = 1\):
t_continua.var()
np.float64(0.9914591886486139)
En cambio, para la distribución discreta, vemos que la varianza crece:
t_redondeada.var()
np.float64(1.0724561136000001)
Esto no es una fluctuación estadística, sino que, bajo ciertas aproximaciones, se puede calcular como la varianza de la variable continua más la varianza de una variable uniforme cuyo ancho está dado por la resolución:
1 + scipy.stats.uniform(0, 1).var()
np.float64(1.0833333333333333)
La varianza de la uniforme \(U[a, b]\) es \(\frac{(b-a)}{12}\).
Si conocieramos la varianza de la variable continua, podriamos estimar a priori la varianza de la variable discretizada que medimos.
donde \(\Delta\) es la resolución de las mediciones.
Generalmente, en el laboratorio estimamos directamente \(\sigma^2_{discreta}\) a partir de las mediciones (ya discretizadas). Podríamos hacer al revés y calcular
para saber lo que podría llegar a medir alguien con un instrumento con mayor resolución.
Nota: la primer formula se puede encontrar en trabajos de microscopía de superresolución, donde \(\sigma^2_{continua}\) es cuanto se dispersan los fotones (difracción, que lo determina el sistema óptico) y \(\Delta\) está dado por el ancho de los pixeles de la cámara (que discretizan la posición donde se detecta el fotón).
Calculando la distribución#
En la sección anterior, comparamos la variable continua y discretizada para una cantidad de muestras fijas. Vimos que hay un aumento en la varianza debido al redondeo de la discretización aunque no parece limitar en cuanto se puede acercar el promedio al valor esperado \(t_0\).
Sin embargo, estos resultados dependen de la cantidad de mediciones \(n\) que usamos.
¿Y cómo cambia esto si variamos los distintos parámetros: el valor de \(t_0\), el ancho \(\sigma\), la resolución \(\Delta\)?
Sin pérdida de generalidad, podemos dejar fijo \(\Delta = 1\) (que es facil de simular) y variar \(\sigma\). En otras palabras, pueden pensar que está todo en unidades de \(\Delta\): cada vez que lean \(\sigma\) es \(\displaystyle \frac{\sigma}{\Delta}\).
Para la cantidad de mediciones, podemos ver que pasa para \(n \to \infty\) calculando la esperanza, para lo que necesitamos la distribución teórica.
Para la distribución continua, vamos a usar:
X = scipy.stats.norm(12.3456, 1)
print(f"{X.mean() = }")
print(f"{X.var() = }")
X.mean() = np.float64(12.3456)
X.var() = np.float64(1.0)
(son exactamente los mismos números que ponemos cuando creamos la variable aleatoria \(X\)).
Para la discreta, vamos a calcular la esperanza \(\text{E}[\cdot]\):
para el promedio,
para la varianza,
para lo cual necesitamos obtener la distribución discreta \(P(x)\).
Para un dado \(x_i\), la probabilidad \(P(x_i)\) de que obtengamos \(x_i\) es la probabilidad de que salga un valor continuo \(x\) que se redondea a \(x_i\):
es decir, la probabilidad de salga un valor en el intervalo \([x_i - \Delta/2, x_i + \Delta/2]\), donde \(f_X(x)\) es la distribución de probabilidad de la variable continua.
def distribucion_discreta(X: scipy.stats.rv_continuous, /):
# Habría que ir desde -infinito a +infinito
# pero alcanza con -10 sigma a 10 sigma
x_min = int(X.mean() - 10 * X.std())
x_max = int(X.mean() + 10 * X.std()) + 1
x = np.arange(x_min, x_max)
prob = X.cdf(x + 0.5) - X.cdf(x - 0.5)
return x, prob
X = scipy.stats.norm(12.345, 1)
x_disc, P_disc = distribucion_discreta(X)
fig, axes = plt.subplots(2, sharex=True)
axes[0].set(xlim=(6, 18), ylabel="Densidad de\nprobabilidad\n$f(x)$")
axes[1].set(xlabel="x", ylabel="Probabilidad\n$P(x)$")
for xi, Pi in zip(x_disc, P_disc):
x = np.linspace(xi - 0.5, xi + 0.5, 100)
axes[0].fill_between(x, X.pdf(x))
axes[1].scatter(xi, Pi)
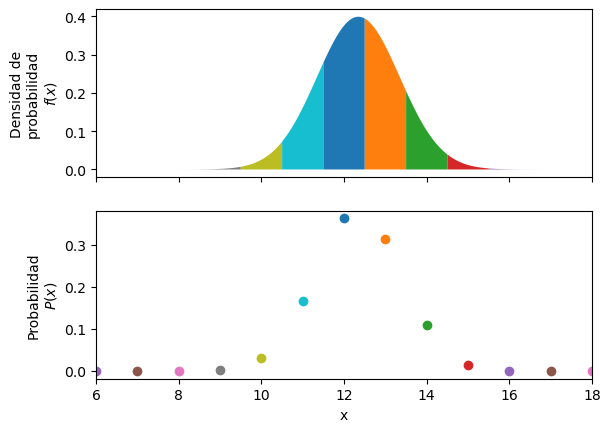
Cada punto de un dado color en la distribución discreta (debajo), corresponde a integrar el area del mismo color en la distribución continua (arriba).
El promedio#
Una vez que tenemos la distribución discreta, podemos calcular la esperanza:
def esperanza(x, prob):
return np.sum(x * prob)
X = scipy.stats.norm(12.345, 1)
x, P = distribucion_discreta(X)
esperanza(x, P)
np.float64(12.344999999295682)
que queda muy cerca del valor \(12.345\) que pusimos como valor «real» (es decir, de la distribución continua).
Calculemos la diferencia entre estos valores, que se conoce como sesgo o bias:
def bias(X: scipy.stats.rv_continuous):
x, P = distribucion_discreta(X)
esperanza_discreta = esperanza(x, P)
esperanza_continua = X.mean()
return esperanza_discreta - esperanza_continua
bias(scipy.stats.norm(12.345, 1))
np.float64(-7.043183813948417e-10)
¡\(10^{-10}\)!
¿Qué significa esto?
Si promediamos cada vez más muestras, el promedio de las muestras discretas (o redondeadas) se acerca a un valor que difiere en \(7 \cdot 10^{-10}\) del valor que obtendriamos con las muestras continuas (o sin redondear).
¿Cómo depende este valor de ese valor real, la esperanza de la variable continua?
t0 = np.linspace(11, 13, 100)
sigma = 1
error = [bias(scipy.stats.norm(ti, sigma)) for ti in t0]
plt.plot(t0, error)
plt.ylabel("Bias\n(esperanza discreta - real)")
plt.xlabel("Esperanza o promedio real")
plt.grid()
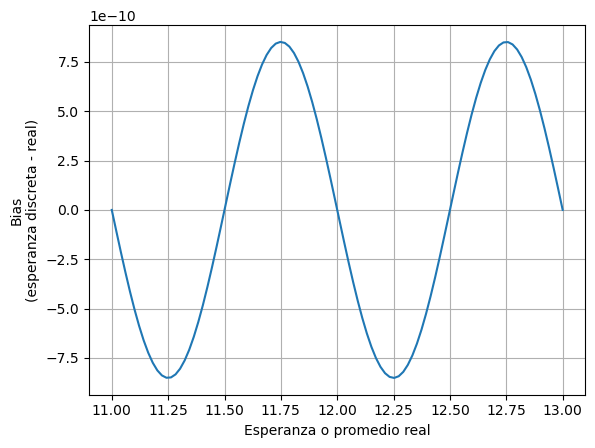
El error no es independiente de ese valor, pero es del mismo orden. Y se hace exactamente 0 cuando el valor real pasa justo por los valores discretos (11, 12, 13), o cuando está justo en el medio de dos valores discretos (11.5, 12.5).
Podemos repetir este gráfico para otros \(\sigma\):
t0 = np.linspace(11, 13, 100)
for sigma in [0.1, 0.2, 0.3]:
error = [bias(scipy.stats.norm(ti, sigma)) for ti in t0]
plt.plot(t0, error, label=sigma)
plt.legend(title=r"$\sigma$")
plt.ylabel("Bias")
plt.xlabel("Promedio real")
plt.grid()
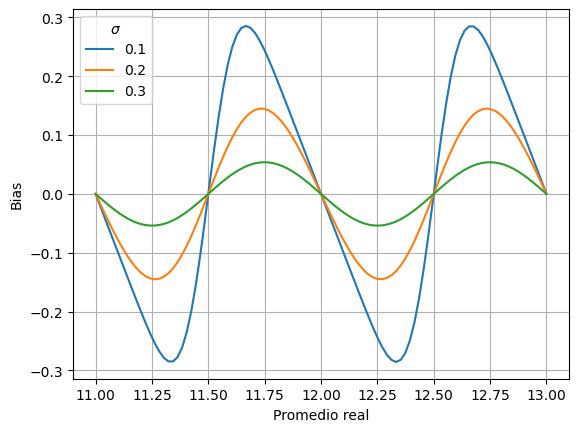
Para estos \(\sigma\) más pequeños, vemos que el bias es mucho mayor, casi del orden de la resolución \(\Delta\).
Entonces, grafiquemos como depende el error de este otro parámetro, \(\sigma\), para un promedio real fijo:
t0 = 11.25
sigma = np.linspace(0.1, 2, 100)
error = [np.abs(bias(scipy.stats.norm(ti, si))) for si in sigma]
plt.plot(sigma, error)
plt.yscale("log")
plt.ylabel("Bias")
plt.xlabel(r"$\sigma$")
plt.grid()
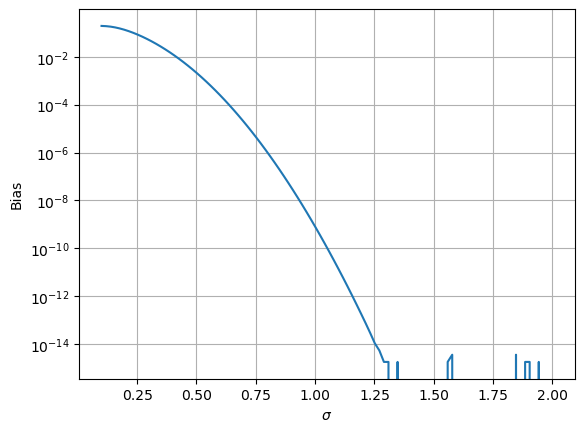
El error cae muy rápidamente (noten la escala logaritmica). Para \(\sigma > 1.25\), ya ni podemos calcularlo, y lo que vemos es producto de errores númericos.
Y, dado que el error del promedio disminuye como \(\frac{\sigma}{\sqrt{N}}\), para \(\sigma=1\) tendríamos que hacer \(N=10^{20}\) mediciones para que nos importara este efecto. ¡Pero, ojo, esto lo estamos calculando para la distribución normal! Para otras distribuciones (en particular, una uniforme) es distinto Kollar[1], Widrow et al.[2].
Entonces, para tener una regla general en mente, veamos como se ve una distribución gaussiana discretizada al variar \(\sigma\):
def plot_dist(axes, sigma: float):
X = scipy.stats.norm(11.25, sigma)
x_disc, P_disc = distribucion_discreta(X)
x_cont = np.linspace(0, 20, 1000)
error = np.abs(bias(X))
axes[0].set_title(f"$\\sigma$ = {sigma}\n\nbias = {error:.2g}")
axes[0].fill_between(x_cont, X.pdf(x_cont))
axes[1].scatter(x_disc, P_disc)
sigmas = [0.1, 0.4, 0.7, 1]
fig, axes = plt.subplots(2, ncols=len(sigmas), sharex=True, figsize=(14, 3))
axes[0, 0].set(xlim=(5, 17))
for ax, s in zip(axes.T, sigmas):
plot_dist(ax, s)
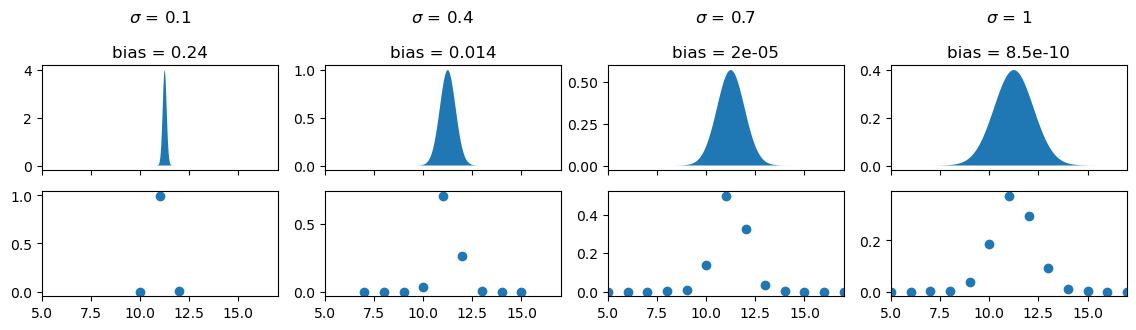
Entonces, para \(\sigma \sim 0.7 \Delta\) (tercer gráfico), vamos a observar 3 o 4 valores discretos contigos (10, 11, 12 y 13, en este caso). El error por discretizar es del orden de \(10^{-5}\), que es lo suficientemente bajo para ignorarlo (es decir, no van a promediar \(10^{10}\) mediciones).
En cambio, si solo observan 2 o 3 valores discretos, hay que tener cuidado en que el promedio no va a tender al valor que queremos estimar realmente.
La varianza#
Todo lo que hicimos para el promedio se puede repetir para la varianza:
def error_varianza(X: scipy.stats.rv_continuous):
x, P = distribucion_discreta(X)
esperanza_discreta = esperanza(x, P)
varianza_discreta = esperanza((x - esperanza_discreta) ** 2, P)
varianza_continua = X.var()
return varianza_discreta - varianza_continua
sigma = np.linspace(0, 2, 100)[1:]
plt.plot(sigma, [error_varianza(scipy.stats.norm(10, s)) for s in sigma])
plt.axhline(scipy.stats.uniform(0, 1).var(), color="black", linestyle="--")
plt.ylabel("Error en la varianza\n(varianza discreta - continua)")
plt.xlabel(r"$\sigma$")
Text(0.5, 0, '$\\sigma$')
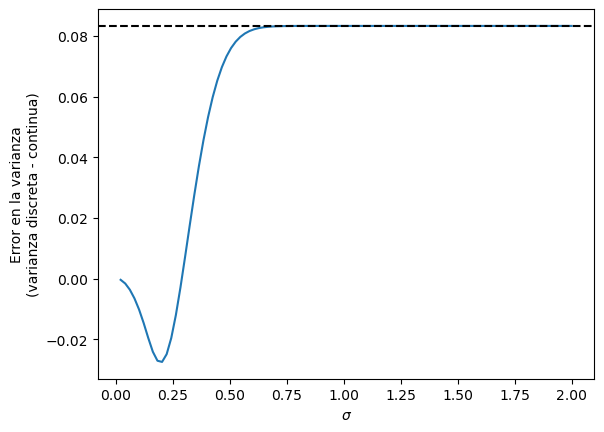
En el gráfico, se ve la diferencia entre la varianza de la variable discreta y continua. A partir de cierto valor, la diferencia tiende al valor de una uniforme de anchor \(\Delta\), como dijimos anteriormente.
¿Siempre queremos calcular un promedio?#
Todo esto que hicimos arriba es para el promedio de muchas muestras. Pero no siempre queremos calcular un promedio.
Por ejemplo, si estamos midiendo el díametro (linea azul) de un círculo y no pasamos exactamente por el centro (punto azul), ya sea que nos desviemos para un lado (linea naranja) o para el otro (linea verde), el valor que midamos va a ser menor.
fig, ax = plt.subplots()
ax.axis(False)
ax.set(xlim=(-1, 1), ylim=(-1, 1), aspect="equal")
ax.scatter(0, 0)
ax.add_patch(plt.Circle((0, 0), 1, facecolor="none", edgecolor="C0"))
ax.axline((-1, 0), slope=0)
ax.axline((-1, 0), slope=0.2, color="C1")
ax.axline((-1, 0), slope=-0.2, color="C2")
<matplotlib.lines.AxLine at 0x7f66b4b0bb90>
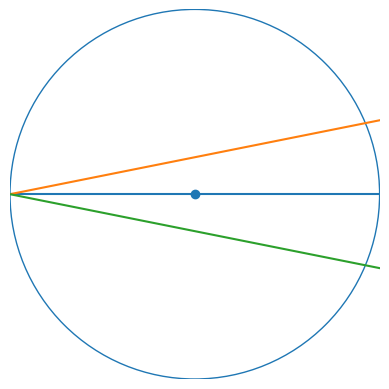
Por lo tanto, el promedio de esas mediciones siempre va a ser menor al valor real. Lo que querríamos es el máximo de las mediciones.
En cambio, si queremos calcular el promedio cuando medimos el periodo del péndulo. Ahí, estamos midiendo la diferencia entre dos variables con la misma distribución, por lo que la distribucion resultante es simétrica alrededor del valor real. Otro día escribo más en detalle sobre esto.
Bibliografía#
Más articulos en: http://users.df.uba.ar/jaliaga/dither/

