Histogramas

import matplotlib.pyplot as plt
import numpy as np

plt.rc("figure", dpi=100, figsize=(6, 3))

Resumen

Dado un conjunto de datos que tenemos en una variable x, por ejemplo, datos que cargmos desde un archivo de texto con x = np.loadtxt("mis_datos.txt"), podemos hacer un histograma de los datos con plt.hist:

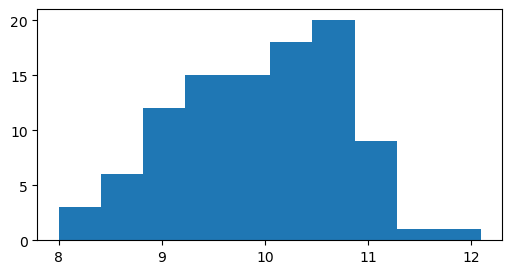
plt.hist(x, bins="auto")

(array([ 3.,  6., 12., 15., 15., 18., 20.,  9.,  1.,  1.]),
 array([ 8.  ,  8.41,  8.82,  9.23,  9.64, 10.05, 10.46, 10.87, 11.28,
        11.69, 12.1 ]),
 <BarContainer object of 10 artists>)

En la siguientes secciones, se explica:

• ¿Qué es un histograma?

• ¿Cómo se grafica un histograma?

• ¿Cómo se elige la cantidad de intervalos o bins?

• ¿Cómo comparar y normalizar histogramas?

• ¿Qué cuidados hay que tener con variables «discretas»?

Histograma

Un histograma es una representación de la distribución de datos numéricos.

Para construir un histograma, primero hay que dividir el rango de los datos en intervalos o bins (del inglés, canastas). Luego, se cuentan cuantos valores caen en cada bin.

NumPy ya incluye una función para esto: np.histogram. Le tenemos que pasar los datos como primer parámetro, y los bordes de los bins como segundo parámetro:

datos = np.array([1, 2, 5, 6, 7, 9])
bordes = np.array([0, 4, 8, 12])

np.histogram(datos, bins=bordes)

(array([2, 3, 1]), array([ 0,  4,  8, 12]))

El primer array que devuelve es la cantidad de datos en cada bin:

• entre 0 y 4, encontró 2 valores,

• entre 4 y 8, encontró 3 valores,

• entre 8 y 12, encontró 1 valor.

El segundo array es el mismo array de bordes que le pasamos.

Devuelve este segundo array porque, en lugar de darle explícitamente bordes, le podemos decir que genere una cantidad de bins:

num_bins = 3
np.histogram(datos, bins=num_bins)

(array([2, 2, 2]), array([1.        , 3.66666667, 6.33333333, 9.        ]))

Noten que cambió la cantidad de valores en cada bin, porque cambió la posición de los bins.

Cuando genera los bins, internamente hace lo siguiente:

num_bordes = num_bins + 1
np.linspace(np.min(datos), np.max(datos), num_bordes)

array([1.        , 3.66666667, 6.33333333, 9.        ])

Es decir, genera los bordes equiespaciados entre el mínimo y máximo de los datos.

Gráfico de histograma

Generalmente, para graficar un histograma, se realiza un gráfico de barras, donde la altura corresponde a la cantidad de valores, y el ancho esta dado por el intervalo que ocupa un bin.

Para realizar un (gráfico de) histograma, pueden usar la función plt.hist de matplotlib:

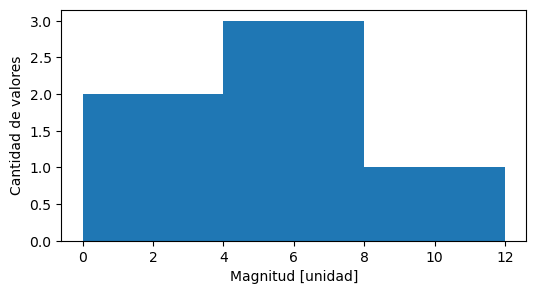
plt.hist(datos, bins=bordes)

plt.xlabel("Magnitud [unidad]")
plt.ylabel("Cantidad de valores")

Text(0, 0.5, 'Cantidad de valores')

Nota

Como los datos son inventados, los nombres de los ejes son genéricos. En un caso particular, pueden poner nombres más explícitos. Por ejemplo, si los datos fuesen de alturas de personas, pueden poner Altura [cm] en el eje x, y Cantidad de personas en el eje y.

Internamente, plt.hist llama la función np.histogram, y usa el resultado para realizar el gráfico de barras.

La primer barra está entre 0 y 4, porque así habíamos definido los bordes para el primer bin, y tiene altura 2, porque hay dos valores ahí.

Si le pasamos la cantidad de bins, va a hacer un gráfico distinto.

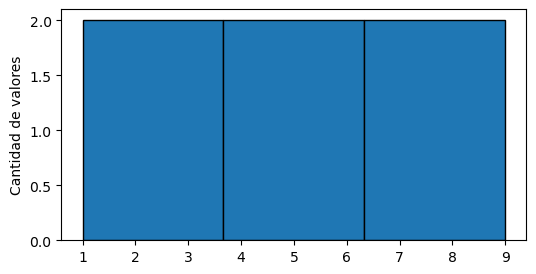
plt.hist(datos, bins=3, edgecolor="black")  # le pintamos los bordes
plt.ylabel("Cantidad de valores")

Text(0, 0.5, 'Cantidad de valores')

Hay una arbitrariedad al elegir la cantidad y posición de los bins. ¿Cuál es el «correcto»?

Cantidad de bins

En general, no tiene sentido hacer un histograma con tan pocos datos.

Para mostrar que sucede al armar un histograma con muchos datos, vamos a usar un generador de números (pseudo)aleatorios.

np.random.seed(0)  # con esto, se repite la secuencia pseudoaleatoria.
datos = np.random.normal(size=3_000)

En la linea anterior, generamos 3000 números con una distribución particular, llamada distribución normal o gaussiana.

Veamos los 5 primeros:

datos[:5]

array([1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799])

Una forma posible de visualizar estos datos es con un gráfico de puntos:

plt.plot(datos, marker=".", linestyle="")

plt.xlabel("Índice del dato")
plt.ylabel("Valor del dato")

Text(0, 0.5, 'Valor del dato')

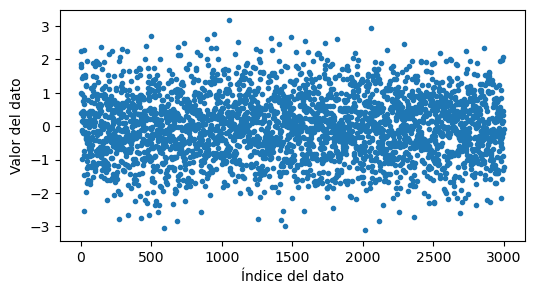
Pero este gráfico no nos permite apreciar la densidad de puntos.

Está claro que hay más puntos en el intervalo \((0, 1)\) que en el intervalo \((3, 4)\).

Pero, ¿hay más puntos en \((0.0, 0.5)\) o en \((0.5, 1.0)\)? ¿O hay aproximadamente la misma cantidad?

Un histograma nos permite contestar esta pregunta.

¿Y cómo elegimos los bins? Una opción, es dejar que los elija automáticamente, en base a un algoritmo:

plt.hist(datos, bins="auto")
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

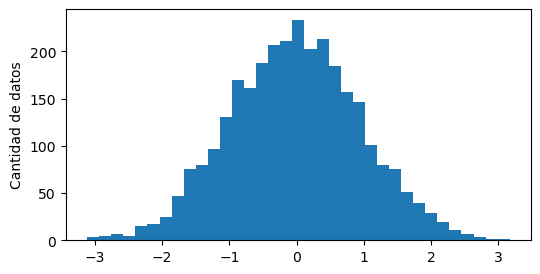
Con este gráfico, podemos entender mejor la distribución de números. Hay más datos alrededor del 0, y la cantidad disminuye a medida que nos alejamos.

Pero la elección automática de bins puede fallar. Veamos que pasa si variamos el número a mano:

fig, axes = plt.subplots(1, 5, figsize=(10, 2))
fig.tight_layout()

for ax, n_bins in zip(axes, (1, 5, 40, 300, 1_000)):
    ax.hist(datos, bins=n_bins)
    ax.set(title=f"#bins = {n_bins}")

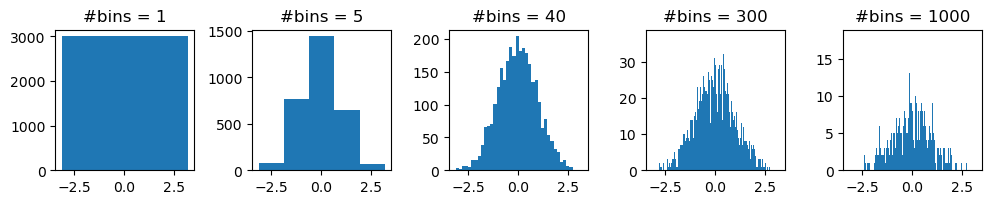
En el primer caso, con un solo bin, solo nos enteramos de:

• la cantidad total de datos, es decir, la altura de la barra,

• el mínimo y el máximo de los datos, el intervalo que cubre la barra.

Si aumentamos a 5 bins, aprendemos un poco más de la distribución: no están uniformemente distribuidos en ese rango, sino que hay más alrededor del centro.

Y si llegamos a 40, vemos que la distribución tiene una forma particular, de campana.

Pero, si seguimos subiendo la cantidad, en algún momento se deja de ver una forma «suave», como en el caso de 300 bins. De un bin al siguiente, cambia significativamente la cantidad de datos.

Y si subimos mucho la cantidad, como en el de 1000 bins, ya se deja de distinguir la forma. Parece más una pirámide que una campana.

En el limite de muchos bins, cada bin tendría un solo dato, y sería como haber hecho el gráfico de puntos que hicimos antes.

En general, la elección de bins va a depender tanto de la cantidad de datos que tengamos como de la distribución que tengan dichos datos.

Comparando histogramas

Graficando múltiples histogramas

Supongamos que tenemos dos series de 1000 datos:

x1 = np.random.normal(loc=0, size=1000)
x2 = np.random.normal(loc=0.5, size=1000)

y queremos comparar sus histogramas.

Al hacer múltiples histogramas, el nuevo histograma tapa el anterior.

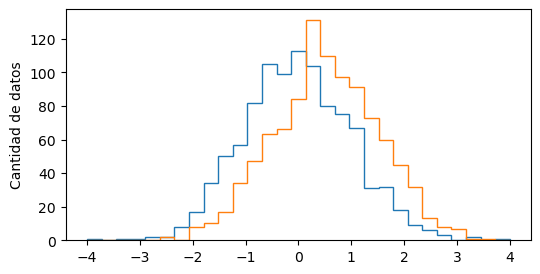
plt.hist(x1, bins=30)
plt.hist(x2, bins=30)
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

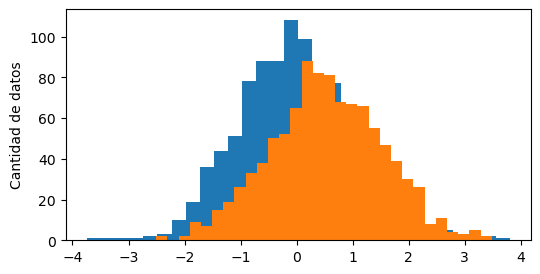
En ese caso, pueden agregarle la opción histtype="step" para cambiar la forma en que grafica:

bins = np.linspace(-4, 4, 30)

plt.hist(x1, bins=bins, histtype="step")
plt.hist(x2, bins=bins, histtype="step")
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

Truco

Para muchos bins, histtype="step" tarda mucho menos en hacer el gráfico.

Normalizando histogramas

Capaz notaron que, en el gráfico anterior, generamos los bins aparte, en lugar de decirle la cantidad de bins a plt.hist.

Esto se debe a que la altura del histograma no solo depende de la cantidad de bins, sino también del ancho de bin. Un bin más ancho engloba más cantidad de datos.

Miremos el siguiente ejemplo, donde graficamos los mismos datos dos veces, pero con distinta cantidad de bins:

x = np.random.normal(loc=0, scale=1, size=1000)

plt.hist(x, bins=10, histtype="step")
plt.hist(x, bins=20, histtype="step")
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

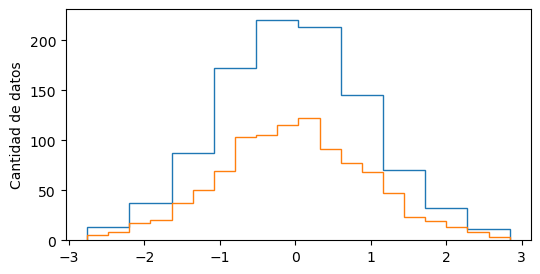
Entonces, si queremos comparar en cantidad de datos, tenemos que usar los mismos bins. No tiene sentido comparar la cantidad de datos en el intervalo \((0, 1)\) contra la de \((0, 5)\).

Pero no siempre nos conviene usar la misma cantidad de bins. Si tenemos dos series de datos con diferente cantidad de datos, 100 y 10.000, vamos a querer graficar el segundo con bins más angostos, para apreciar mejor su forma.

Para esos casos, podemos normalizar el histograma con el parámetro density=True:

plt.hist(x, bins=10, histtype="step", density=True)
plt.hist(x, bins=20, histtype="step", density=True)
plt.ylabel("Densidad de fracción de valores")

Text(0, 0.5, 'Densidad de fracción de valores')

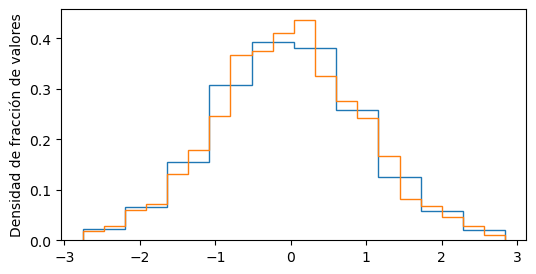
La normalización es tal que el área de cada bin, es decir, su ancho por su altura, es la fracción de valores que cayeron ahí. Por lo tanto, la suma de las áreas da 1 (o, 100%).

Advertencia

Esta normalización solo es válida para variables continuas. Si queremos normalizar un histograma de variables discretas, como el resultado de tirar muchas veces un dado, la normalización tiene que ser tal que la suma de las alturas (no el área) sea 1.

Si se fijan atentamente, cada bin azul es el promedio de los dos bins naranjas que abarca. Pero justo porque estamos comparando 10 contra 20 bins y quedan alineados.

Extra

Datos truncados

En física, generalmente trabajamos con datos continuos, como tiempos o longitudes. Sin embargo, cuando medimos tenemos una precisión finita, y las mediciones se truncan a una cierta cantidad de dígitos. Esto puede traer problemas al hacer un histograma si el ancho de bin es del orden de dicha precisión.

Por ejemplo, supongamos que medimos con un cronómetro que mide a la décima de segundo. Un valor de tiempo «real» \(t=3.141592... \text{ s}\) lo mediríamos como \(t=3.1 \text{ s}\). Podemos simular esto con la función np.round:

np.round(3.141592, 1)

3.1

Entonces, generemos muchos datos, redondeémoslos, y comparemos sus histogramas.

x = np.random.normal(loc=0, scale=1, size=10_000)
y = np.round(x, 1)

Caso 1: bins más chicos que la resolución

ancho_bin = 0.08
bins = np.arange(np.min(y), np.max(y), ancho_bin)

fig, axes = plt.subplots(2, 1, sharex=True)
axes[0].hist(x, bins=bins, label="Sin redondear")
axes[1].hist(y, bins=bins, label="Redondeados")
for ax in axes:
    ax.set(ylabel="Cantidad de datos")
    ax.legend()

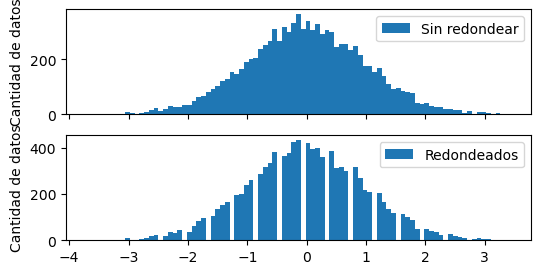
La forma del histograma es parecida, pero el redondeado tiene huecos cada tanto.

Esto se debe a que el ancho de bin, 0.08, ligeramente más chico que la resolución, 0.1, cada cierta cantidad de bins, un bin no encuentra ningún valor en ese rango.

Por ejemplo, si un bin va de 0.03 a 0.11, el siguiente va a ir de 0.11 a 0.19, y no va a encontrar ninguna medición ahí. Las mediciones que cayeron en ese rango se redondearon a 0.1 o 0.2.

Caso 2: bins más grandes que la resolución

ancho_bin = 0.14
bins = np.arange(np.min(y), np.max(y), ancho_bin)

fig, axes = plt.subplots(2, 1, sharex=True)
axes[0].hist(x, bins=bins, label="Sin redondear")
axes[1].hist(y, bins=bins, label="Redondeados")
for ax in axes:
    ax.set(ylabel="Cantidad de datos")
    ax.legend()

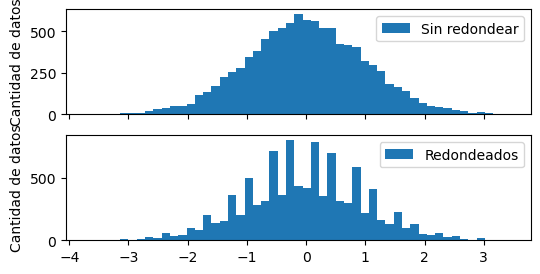
En este caso, no hay huecos en el histograma, pero se ven estos picos con muchos más datos que sus vecinos.

Al redondear, los datos solo pueden caer en lugares discretos, múltiplos de la resolución, 0.1. Al ser el ancho de bin un poco más grande que la resolución, cada cierta cantidad de bins, un bin abarca dos de estos lugares discretos.

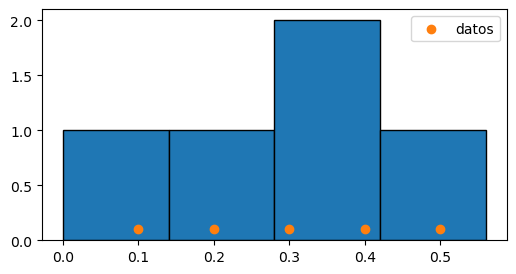
Pueden ver lo mismo en este caso más simple, con datos equiespaciados en 0.1, y pero bins de ancho 0.14:

datos = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
bordes = 0.14 * np.array([0, 1, 2, 3, 4])

plt.hist(datos, bordes, edgecolor="k")
plt.scatter(datos, np.full_like(datos, 0.1), color="C1", label="datos")
plt.legend()

bordes

array([0.  , 0.14, 0.28, 0.42, 0.56])

Caso 3: bins proporcionales a la resolución

Si usamos un múltiplo de la resolución para el ancho de bin, se resuelve el problema que mencionamos:

resolucion = 0.1

ancho_bin = 2 * resolucion
bins = np.arange(np.min(y), np.max(y), ancho_bin)
plt.hist(y, bins=bins, density=True, histtype="step", label="Sí - x2")

ancho_bin = 2.5 * resolucion
bins = np.arange(np.min(y), np.max(y), ancho_bin)
plt.hist(y, bins=bins, density=True, histtype="step", label="No - x2.5")

plt.legend(title="Múltiplo de la resolución")
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

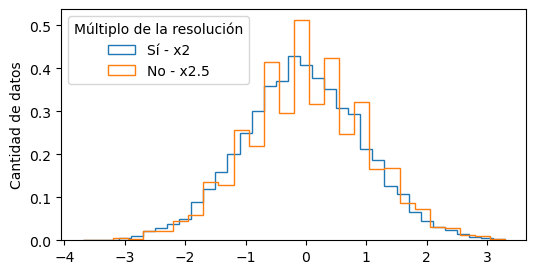
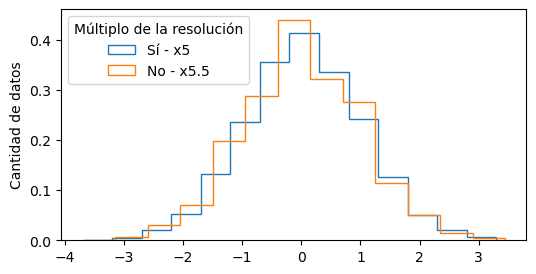
Este problema no es tan relevante cuando el ancho de bin es mucho mayor a la resolución de nuestras mediciones.

Por ejemplo, con un ancho de ~5 veces la resolución, ya no es tan relevante:

resolucion = 0.1

ancho_bin = 5 * resolucion
bins = np.arange(np.min(y), np.max(y), ancho_bin)
plt.hist(y, bins=bins, density=True, histtype="step", label="Sí - x5")

ancho_bin = 5.5 * resolucion
bins = np.arange(np.min(y), np.max(y), ancho_bin)
plt.hist(y, bins=bins, density=True, histtype="step", label="No - x5.5")

plt.legend(title="Múltiplo de la resolución")
plt.ylabel("Cantidad de datos")

Text(0, 0.5, 'Cantidad de datos')

Si llegaran a tener este problema, acá les dejamos una función para generar \(N\) bins para datos truncados por la resolución:

def generar_bins_truncados(datos, resolucion: float, n_bins: int):
    """Genera bins para datos truncados a una dada resolución."""
    # Como el ancho de bin va a ser un múltiplo de la resolución,
    # le sumo y resto media resolución a los extremos,
    # para no tener problemas numéricos en los bordes de los bins.
    x_min = np.min(datos) - resolucion / 2
    x_max = np.max(datos) + resolucion / 2
    # El paso para dividir el intervalo en n_bins
    paso = (x_max - x_min) / n_bins
    # que convierto en un múltiplo de la resolución
    paso = np.ceil(paso / resolucion) * resolucion
    bins = x_min + paso * np.arange(n_bins + 1)
    return bins


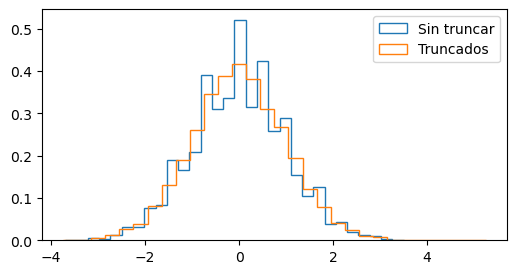
n = 30
plt.hist(y, bins=n, histtype="step", density=True, label="Sin truncar")
plt.hist(
    y,
    bins=generar_bins_truncados(y, resolucion=0.1, n_bins=n),
    histtype="step",
    density=True,
    label="Truncados",
)
plt.legend()

<matplotlib.legend.Legend at 0x7fa7125675b0>