Error sistemático y modelado

Error sistemático y modelado#

Bajo la aproximación de pequeñas oscilaciones, el periodo de oscilación \(T\) de un péndulo de largo \(L\) es:

(1)#\[ T = 2π \sqrt{\frac{L}{g}} \]

donde \(g\) es la aceleración de la gravedad.

Si medimos el periodo \(T\) para múltiples largos \(L\), podemos obtener \(g\) a partir de un ajuste por cuadrados mínimos, ya sea que ajustemos por la ecuación (1) o por su cuadrado:

(2)#\[ T^2 = (2π)^2 \, \frac{L}{g} \]

En la práctica, se suele observar que hay que agregar una constante al ajuste. Sin embargo, no es lo mismo agregar una constante en (2)

(3)#\[ L = g \left( \frac{T}{2π} \right)^2 + L_0 \]

que en (1)

\[ \sqrt{L} = \sqrt{g} \left( \frac{T}{2π} \right) + B \]

En (2), se puede interpretar esta constante \(L_0\) como un error sistemático en la longitud \(L\). En cambio, en (1), se podría reinterpretar \(B\) como un error sistemático \(T_0\) en el periodo \(T\)

(4)#\[ L = g \left( \frac{T+T_0}{2π} \right)^2 \]

Veamos que sucede si simulamos uno de estos casos y ajustamos por los modelos incorrectos.

Hide code cell content 
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit


def ajustar(func, x, y, yerr=None, **kwargs):
    """Ajusta con curve_fit y devuelve los errores
    en lugar de la matriz de covarianza."""
    p, cov = curve_fit(func, x, y, sigma=yerr, **kwargs)
    err = np.sqrt(np.diag(cov))
    return p, err


def graficar_ajuste(x, y, y_pred, yerr=None, *, color="C0", fig=None, axes=None):
    """Grafica el ajuste y los residuos."""
    if axes is None:
        if fig is None:
            fig = plt.figure()
        axes = fig.subplots(2, sharex=True)

    axes[0].errorbar(x, y, yerr, fmt="o", capsize=5, color=color)
    axes[0].plot(x, y_pred, color=color)
    axes[1].errorbar(x, y - y_pred, yerr, fmt="o", capsize=5, color=color)
    axes[1].axhline(0, color=color)
    return axes

g = 9800  # mm/s


def periodo(L, g):
    """Periodo del péndulo en la aproximación de pequenas oscilaciones.

    T = 2π √(L/g)
    """
    return 2 * np.pi * np.sqrt(L / g)

Simulando una medición#

Para entender que pasa al analizar incorrectamente las mediciones, por ejemplo, cuando se ignora el efecto del error sistemático en la longitud, necesitamos simular correctamente el proceso de medición.

Hipótesis#

Para la simulación, vamos a asumir dos cosas:

  1. tenemos un error sistemático \(L_0\) en la longitud \(L\),

  2. el error en el periodo \(T\) es despreciable frente al error en la longitud \(L\).

Este último punto es razonable, ya que podemos medir muchos periodos para una dada longitud, y reducir el error de \(T\). En cambio, al medir \(L\), estamos limitados por el error de resolución \(\Delta L\) de la cinta métrica.

Error por resolución en la longitud \(L\)#

Al preparar el experimento, se arma el péndulo de una dada longitud \(L_{real}\), que cuya medición \(L_{medido}\) se determina con una dada precisión \(\Delta L\). Entonces, para simular la medición, vamos a generar un $L_{real} y redondearlo. Por ejemplo,

\[\begin{split} \begin{aligned} L_{real} &= 500.325\ldots \text{ mm} \\ L_{medido} &= 500 \text{ mm} \\ \Delta L &= 1 \text{ mm} \end{aligned} \end{split}\]

donde asumimos que medimos con una cinta metrica de \(1 \text{ mm}\) de resolución.

Por otro lado, el periodo \(T_{real}\) lo tenemos que calcular a partir del \(L_{real}\), no del \(L_{medido}\). Después de todo, el péndulo (o la naturaleza) sí conoce el largo real. Y el periodo medido \(T_{medido}\), como asumimos que podemos hacer muy pequeño el error, va a ser igual al real: \(T_{medido} = T_{real}\).

Con un error sistemático \(L_0\)#

Para considerar un error sistemático \(L_0\), se lo sumamos al \(L_{real}\) antes de «medir» (redondear):

\[\begin{split} \begin{aligned} L_{real} &= 500.325\ldots \text{ mm} \\ L_0 &= 0.431\ldots \text{ mm} \\ L_{medido} &= 501 \text{ mm} \\ \Delta L &= 1 \text{ mm} \end{aligned} \end{split}\]

Al igual que antes, el \(T_{real}\) se calcula a partir del \(L_{real}\), sin considerar el error sistemático ni la medición.

Hide code cell content 
def experimento(*, L_min=300, L_max=1000, N_largos=10, L0=0, decimales=0):
    def medir():
        ΔL = 10 ** (-decimales)
        # Los valores reales
        # Al L real, para que no sea exactamente igual al medido cuando redondeemos,
        # y varie en las repeticiones del experimento,
        # le agregamos una pequeña desviación, tal que sus decimales no sean 0.
        L_real = np.linspace(L_min, L_max, N_largos)
        L_real += np.random.uniform(-ΔL / 2, ΔL / 2, size=N_largos)
        T_real = periodo(L_real, g=g)

        # Los valores medidos:
        # - el T medido no tiene error, así que lo dejamos igual al T real
        # - el L medido proviene de redonear el L real + un error sistemático L0
        T_medido = T_real
        L_medido = np.round(L_real + L0, decimales)

        # El error para L equivalente a una desviación estándar es:
        L_err = ΔL / 12**0.5
        L_err = np.full(N_largos, L_err)

        return T_medido, L_medido, L_err, L_real

    return medir

Efecto del error sistemático#

Al realizar una simulación, tenemos acceso a los valores reales, sin «error de medición». Antes de hacer ajustes, podemos comparar las «mediciones» contra los valores reales. Para eso, vamos a realizar simulaciones para diferentes parámetros, y gráficar tanto \(L\) vs \(T^2\) como \(\sqrt{L}\) vs \(T\).

Hide code cell content 
def graficar_vs_real(medir):
    """Realiza una medición y realiza un gráfico con residuos,
    tanto para T^2 vs L como T vs √L."""
    T, L, L_err, L_real = medir()

    figs = plt.figure(figsize=(8, 3)).subfigures(ncols=3, width_ratios=[1, 0.3, 1])

    # T^2 vs L
    figs[0].suptitle("$L$ vs $T^2$")
    axes = graficar_ajuste(x=T**2, y=L, y_pred=L_real, yerr=L_err, fig=figs[0])
    axes[0].set(ylabel="L [mm]")
    axes[1].set(ylabel="Residuos [mm]", xlabel="T² [s²]")

    # T vs L^1/2
    figs[2].suptitle(r"$\sqrt{L}$ vs $T$")
    axes = graficar_ajuste(
        x=T, y=L**0.5, y_pred=L_real**0.5, yerr=L_err / 2 / L**0.5, fig=figs[2]
    )
    axes[0].set(ylabel=r"$\sqrt{L}$ [√mm]")
    axes[1].set(ylabel="Residuos [√mm]", xlabel="T [s]")

    for fig in figs:
        fig.align_ylabels()

Sin error sistemático#

Si no tenemos error sistemático, en ambos gráficos se observa una relación lineal, y los residuos se distribuyen aleatoriamente alrededor del 0.

graficar_vs_real(experimento(L_min=50, N_largos=30, L0=0))
../_images/02ba4dcbcbb62a0f2fc8e3e1c1e6d2c51f857fc626c7215611a136bc228be094.png

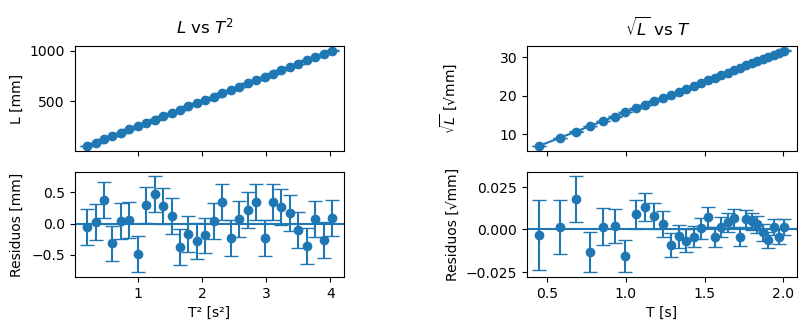
Error sistemático en la longitud#

Si simulamos un error sistemático pequeño, \(L_0 = 1 \text{ mm}\), vemos que la estructura en los residuos es diferente en cada caso.

Para \(L\) vs \(T^2\), podemos se distribuyen aleatoriamente alrededor de \(1\), correspondiendo al error sistemático añadido. Esto se podría corregir agregando una constante, como en (3).

En cambio, para \(\sqrt{L}\) vs \(T\), los residuos no se distribuyen aleatoriamente alrededor de un número. Por lo que no se podría corregir añadiendo una constante, como en (4).

graficar_vs_real(experimento(L_min=50, N_largos=30, L0=1))
../_images/64806823e468f75f38c3ef42f4ae7a1b18fba3d915e04c2552fe9a319ca2163c.png

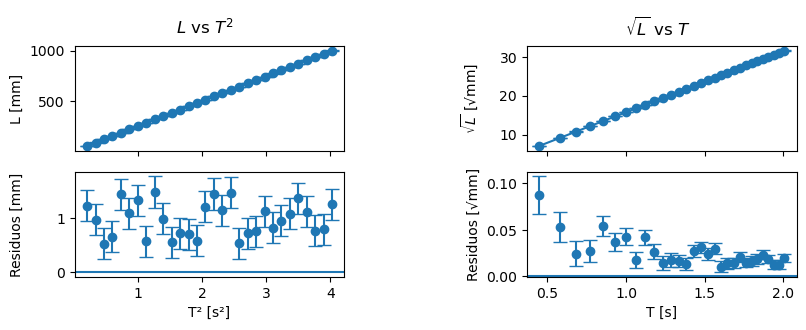
Rango de longitudes medidas#

Con el mismo \(L_0\) que en caso anterior, pero cambiando el rango de longitudes medidas, no observamos una diferencia en la estructura de los residuos en ambos casos. A priori, ambos podrían ajustarse con los modelos (3) y (4), a pesar de que este último es incorrecto.

graficar_vs_real(experimento(L_min=500, N_largos=30, L0=1))
../_images/23a85c0530d57e49bcf7f27e209e4ecc450cb0a36ff6191bfdf22b6e76cf3468.png

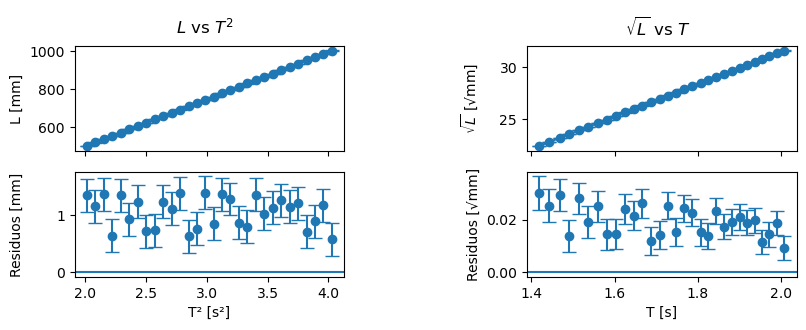
Aumentando la precisión en \(L\)#

Si aumentamos la precisión de medición de \(L\), pasando de un \(\Delta L = 1 \text{ mm}\) a \(\Delta L = 0.1 \text{ mm}\), volvemos a distinguir entre ambos casos.

graficar_vs_real(experimento(L_min=500, N_largos=30, L0=1, decimales=1))
../_images/85c6ab551caab5138672a2e282beb53e50b3bccbd9b6c3b7cdd16f97c9d7d83c.png

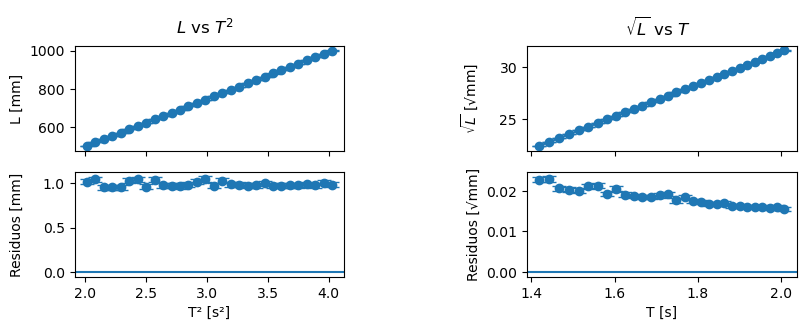
Ajustes y el \(g\) estimado#

Realicemos simulaciones para diferentes parámetros experimentales y observemos que sucede con la estimación de \(g\).

Definamos 3 funciones para ajustar, correspondientes a las ecuaciones (1), (3) y (4).

def sin_constante(T, g):
    Tp = T / (2 * np.pi)
    return g * Tp**2


def sistematico_longitud(T, g, L_0):
    Tp = T / (2 * np.pi)
    return g * Tp**2 + L_0


def sistematico_periodo(T, g, T_0):
    Tp = T / (2 * np.pi)
    return g * (Tp + T_0) ** 2

En lo siguiente, simularemos una medición y ajustaremos las 3 funciones, gráficando el ajuste y los residuos. Además, repetiremos estre proceso \(N=1000\) veces, graficaremos histogramas de la estimación de \(g\) para cada uno de estos modelos.

Hide code cell content 
def repetir_experimentos(medir, N_experimentos=1000):
    def create_plot_axes(fig):
        ax_plot, *ax_residuos = fig.subplots(4, sharex=True)
        ax_plot.set(ylabel="Longitud [mm]")
        for ax in ax_residuos:
            ax.set(ylabel="Residuos [mm]")
        ax.set(xlabel="Periodo [s]")
        fig.align_ylabels()
        return ax_plot, ax_residuos

    def create_hist_axes(fig):
        _, fig = fig.subfigures(2, height_ratios=[1, 4])
        ax = fig.subplots()
        ax.set(xlabel="Ac. de la gravedad [mm/s]")
        return ax

    def ajustar_y_graficar(func, T, L, L_err, *, color, ax_plot, ax_residuos):
        p, err = ajustar(func, T, L, L_err)
        L_pred = func(T, *p)

        ax_plot.plot(T, L_pred, color=color, linestyle="--")
        ax_residuos.errorbar(T, L - L_pred, L_err, fmt="o", capsize=5, color=color)
        ax_residuos.axhline(0, color=color)

    figs = plt.figure(figsize=(8, 6)).subfigures(ncols=2)
    ax_plot, ax_residuos = create_plot_axes(figs[0])
    ax_hist = create_hist_axes(figs[1])

    labels = ("Sin constante", "Longitud $L_0$", "Tiempo $T_0$")
    funcs = (sin_constante, sistematico_longitud, sistematico_periodo)
    colors = ("C0", "C1", "C2")

    T, L, L_err, _ = medir()
    ax_plot.errorbar(T, L, L_err, fmt="o", capsize=5, color="black")
    for ax, func, color in zip(ax_residuos, funcs, colors):
        ajustar_y_graficar(
            func,
            T,
            L,
            L_err,
            color=color,
            ax_plot=ax_plot,
            ax_residuos=ax,
        )

    def analisis_multiple():
        T, L, L_err, _ = medir()
        p0, _ = ajustar(sin_constante, T, L, L_err)
        p1, _ = ajustar(sistematico_longitud, T, L, L_err)
        p2, _ = ajustar(sistematico_periodo, T, L, L_err)
        return p0[0], p1[0], p2[0]

    p = np.array([analisis_multiple() for _ in range(N_experimentos)])

    ax_hist.axvline(g, color="black", label="Valor real")
    for label, pi in zip(labels, p.T):
        ax_hist.hist(pi, bins="auto", histtype="step", label=label)
    ax_hist.legend(loc="lower left", bbox_to_anchor=(0, 1))

Sin error sistemático#

Al no tener error sistemático, los tres modelos ajustan bien a las mediciones, a juzgar por los gráficos de los residuos. Con respecto a los histogramas de \(g\), en los tres casos se encuentran centrados alrededor del valor real. Sin embargo, hay una mayor variación en los valores obtenidos para los modelos con constante.

repetir_experimentos(experimento(L_min=100, L0=0, N_largos=30))
../_images/b5057cb7e813ad31a157ea0420b16f916f5bfb88aa84bd012f06d258d4dca67a.png

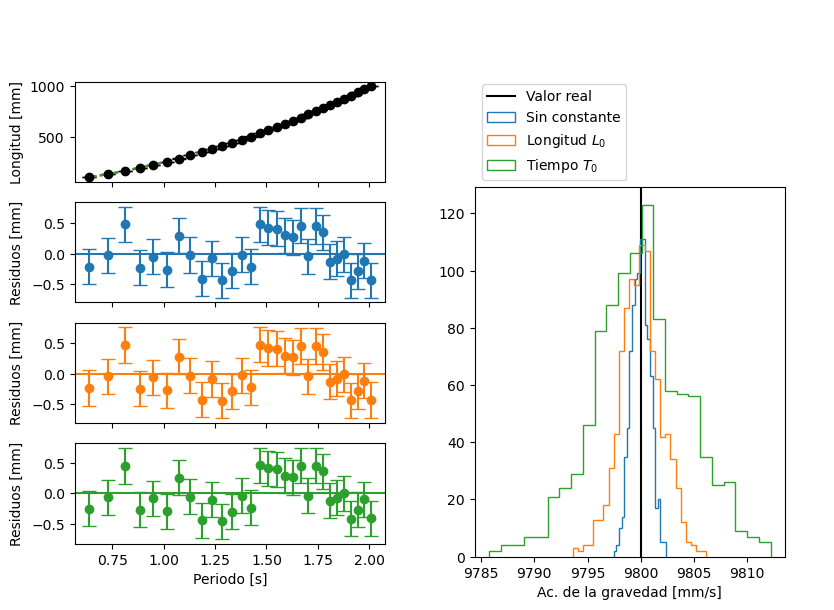
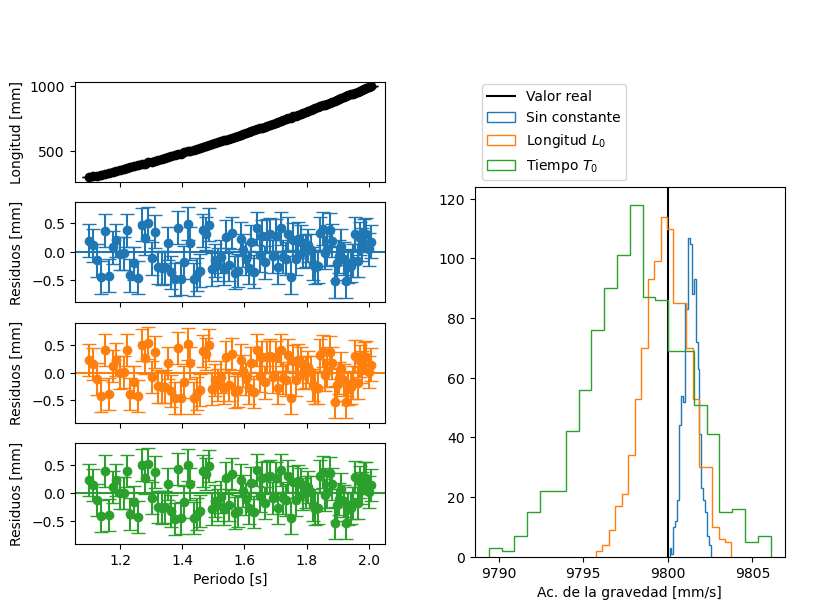
Error sistemático grande#

Si tenemos un error sistemático «grande», \(L_0 = 5 \text{ mm}\), vemos que solo el ajuste que incluye un \(L_0\) tiene residuos sin estructura. En los histogramas de \(g\), vemos que los valores obtenidos en las sucesivas repeticiones están centrados en el valor real para dicho modelo. En cambio, para el modelo sin constante, o el que modela un error sistemático en el periodo, los histogramas se encuentran corridos. En ninguna iteración, sus valores coincidieron con el valor real.

repetir_experimentos(experimento(L_min=100, L0=5, N_largos=30))
../_images/6cf24f9b9fb5606181aa995819c2aab164957795dd8c44f5a5b07a82c57ca72f.png

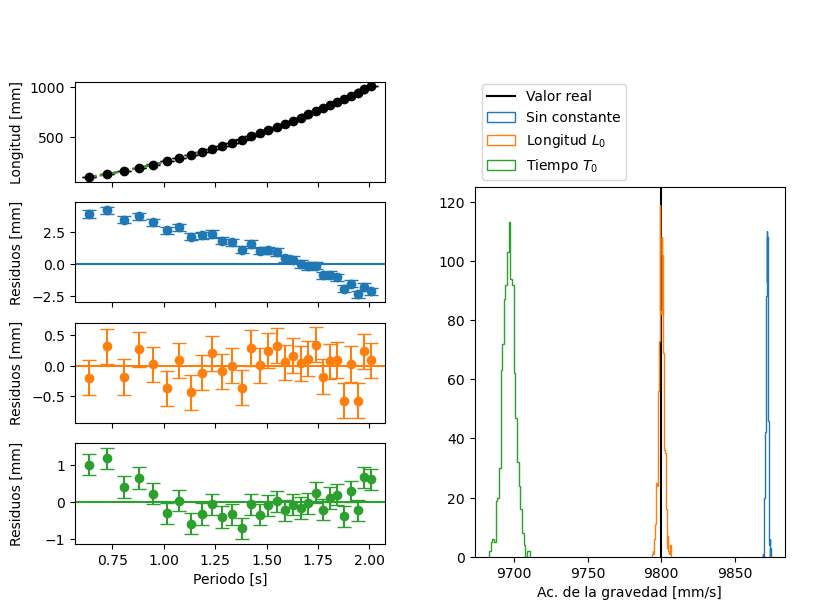
Rango de longitudes medidas#

Si achicamos el rango de longitudes medidas, alejándonos de \(L=0\), el modelo que incluye un error sistemático en \(T_0\) también ajustaría bien, a juzgar por el gráfico de residuos. Sin embargo, según el histograma, vemos que tiene un sesgo en la estimación de \(g\): siempre estima un valor menor.

repetir_experimentos(experimento(L_min=500, L0=5, N_largos=30))
../_images/294b5e733feb3190ff5f78386647b995badfc7147042b7e9118d516e688f3a90.png

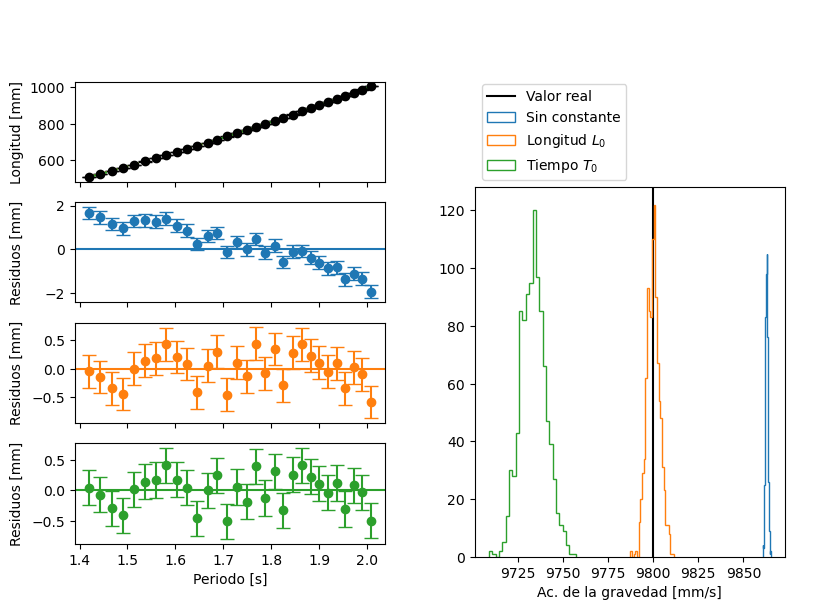
Error sistemático pequeño#

Consideramos un error sistemático pequeño, \(L_0 = 0.1 \text{ mm}\), \(10\) veces menor que la resolución \(\Delta L = 1 \text{ mm}\) de medición.

Si medimos para pocas longitudes, \(N=10\), se observa un ligero sesgo en el ajuste sin constante, pero no muy significativo.

repetir_experimentos(experimento(L_min=300, L0=0.1, N_largos=10))
../_images/032b96390a3ff7dbfdfe0401def6eb59db402b68909f9619405eecb8e9f27502.png

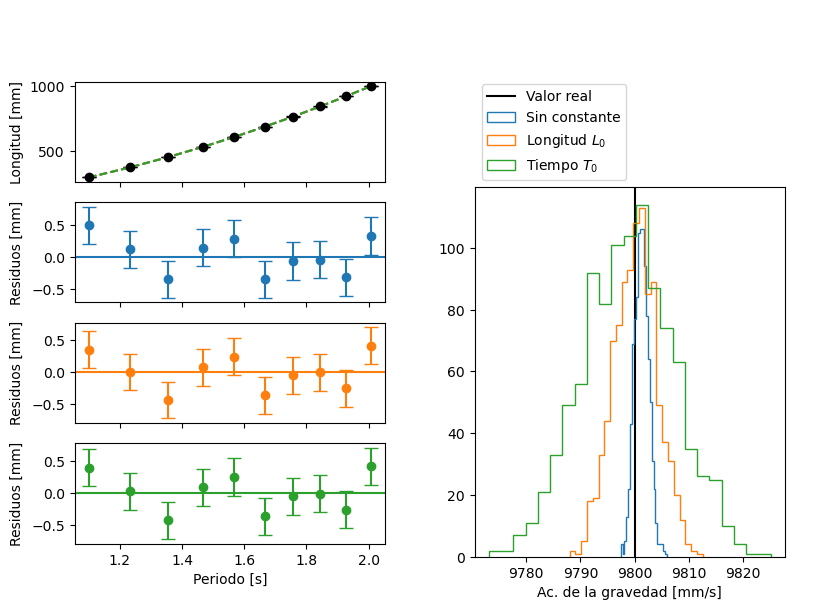
En cambio, si medimos para más longitudes, \(N=100\), el sesgo se incrementa en los modelos incorrectos. En particular, para el modelo sin constante siempre se obtuvo valores de \(g\) superiores al real.

repetir_experimentos(experimento(L_min=300, L0=0.1, N_largos=100))

/tmp/ipykernel_1998/3907591550.py:9: OptimizeWarning: Covariance of the parameters could not be estimated
  p, cov = curve_fit(func, x, y, sigma=yerr, **kwargs)
../_images/375afd773634598b9b464f95164729763c823d2a0a990d96e3b808abb9b991be.png
Contenido