Array (parte 1)

Contenido

Array (parte 1)#

Motivación: graficar funciones#

Para graficar una función \(y = f(x)\) en un dado rango de \(x\), tenemos que:

elegir algunos valores \(x_i\) en ese rango,
calcular \(y_i = f(x_i)\),
graficar los puntos \((x_i, y_i)\) y unirlos con lineas.

Para el primer punto, podríamos guardar los \(x_i\) en una lista:

x = [0, 1, 2, 3]

Para el segundo punto, podríamos recorrer dicha lista, aplicar la función a cada valor, y guardar el resultado en otra lista.

Por ejemplo, para \(f(x) = x^2\):

y = []
for xi in x:
    yi = xi**2
    y.append(yi)

y

[0, 1, 4, 9]

Pero, se puede hacer de una manera mucho más simple (y rápida) utilizando un array de NumPy.

Importando paquetes y módulos#

Para poder reutilizar valores, los asignamos en variables.

Para poder reutilizar bloques de código, definimos funciones, que nos permiten volver a correrlos cambiando algunas variables (parámetros).

Para poder reutilizar funciones, hay que crear módulos, que nos permiten «importar» variables y funciones, y reutilizarlas en diferentes proyectos.

Hasta ahora, estuvimos usando funciones, como print y len, que vienen «pre-importadas» en Python.

Python incluye varios módulos, donde hay funcionalidad extra que nos puede ser útil.

Por ejemplo, el módulo math, que podemos importar así:

import math

Ahora, tenemos una variable math que contiene el módulo math:

math

<module 'math' from '/home/runner/work/python-tutorial/python-tutorial/.pixi/envs/default/lib/python3.10/lib-dynload/math.cpython-310-x86_64-linux-gnu.so'>

Para acceder a las variables y funciones dentro de math, hay que agregar math. antes.

Por ejemplo, la constante \(\pi\) está definida dentro de math:

math.pi

3.141592653589793

y la función coseno:

math.cos(0)

1.0

Hay otros módulos que no vienen pre-incluidos en Python, y hay que instalarlos aparte.

Los que vamos a usar, numpy y matplotlib, ya vienen pre-instalados en Google Colab.

import matplotlib.pyplot as plt
import numpy as np

Como el nombre del módulo es muy largo, se le puede asignar un alias con el as.

La convención es llamar np a numpy y plt a matplotlib.pyplot.

Entonces, en la variable plt está el (sub)módulo pyplot de matplotlib:

plt

<module 'matplotlib.pyplot' from '/home/runner/work/python-tutorial/python-tutorial/.pixi/envs/default/lib/python3.10/site-packages/matplotlib/pyplot.py'>

que nos permitirá realizar gráficos.

Al igual que el módulo math, NumPy también define la constante \(\pi\):

np.pi

3.141592653589793

y la función coseno:

np.cos(0)

1.0

¿Por que vamos a usar NumPy en lugar del módulo math?

Porque, como veremos más adelante, las funciones de NumPy nos permiten operar sobre arrays.

Creación de arrays#

Para crear un array, le podemos pasar una lista a la función np.array:

x = [2, 3, 5]
x = np.array(x)

x

array([2, 3, 5])

También hay diversas funciones que permiten crear arrays comúnmente utilizados.

Por ejemplo, un array de \(n\) ceros:

np.zeros(5)

array([0., 0., 0., 0., 0.])

o funciones para crear rangos de números, como:

arange(start, stop, step)
linspace(start, stop, num)

La primera es análoga a range(start, stop, step), que crea números desde start, hasta (pero sin incluir) stop, separados por un paso step:

np.arange(0, 10, 2)

array([0, 2, 4, 6, 8])

La segunda nos permite especificar la cantidad de números, num, en lugar del paso entre números:

np.linspace(0, 10, 5)

array([ 0. ,  2.5,  5. ,  7.5, 10. ])

y los genera equiespaciados entre start y stop.

Es decir, genera un paso step = (stop - start) / num.

Ejercicio 1#

Crear un array de 9 números equiespaciados en el intervalo \([-1, 1]\).

# Escriba su solución aquí

Solución#

Accediendo a y modificando elementos#

El array es similar a la lista, y comparten ciertos comportamientos.

x = np.array([2, 3, 5])

x

array([2, 3, 5])

Al igual que una lista, se puede acceder al primer elemento como:

x[0]

O reasignar el segundo elemento:

x[1] = 7

x

array([2, 7, 5])

Pero, a diferencia de la lista, no se puede cambiar la cantidad de elementos, ya sea borrando:

del x[0]

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[20], line 1
----> 1 del x[0]

ValueError: cannot delete array elements

o agregando nuevos elementos al final:

x.append(7)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[21], line 1
----> 1 x.append(7)

AttributeError: 'numpy.ndarray' object has no attribute 'append'

Entonces, ¿qué tiene de bueno el array?

Operaciones elemento a elemento y broadcasting#

El array de NumPy nos permite hacer operaciones aritméticas entre elementos sin tener que recorrer el array con un for-loop.

Por ejemplo, si tenemos dos arrays x e y:

x = np.array([1, 2, 3])
y = np.array([10, 20, 30])

podemos calcular la suma elemento a elemento, x[i] + y[i], como:

x + y

array([11, 22, 33])

Para el caso de la suma, es igual a la suma vectorial, si piensan los arrays como vectores.

Pero también funciona con otras operaciones, que no están definidas para vectores:

x * y

array([10, 40, 90])

Si los arrays tienen diferente tamaño, nos arroja un error:

np.array([1, 2, 3]) + np.array([1, 2])

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[25], line 1
----> 1 np.array([1, 2, 3]) + np.array([1, 2])

ValueError: operands could not be broadcast together with shapes (3,) (2,) 

Pero, ¿qué sucede si queremos sumarle un número a x?

x + 1

array([2, 3, 4])

A esto le llama broadcasting, que consiste en «estirar» el 1 hasta que tenga el mismo largo que x, y realizar la suma elemento a elemento.

Funciona para todas las operaciones aritméticas, y permite escribir el código de manera más simple, como si estuviésemos trabajando con un solo número.

2 * x

array([2, 4, 6])

x**2

array([1, 4, 9])

NumPy también define ciertas funciones matemáticas que saben operar sobre arrays, es decir, elemento a elemento:

np.exp(x)

array([ 2.71828183,  7.3890561 , 20.08553692])

Por ejemplo, si definimos un array de ángulos (en radianes), podemos calcular el seno de cada ángulo como:

angulos = np.pi * np.array([0, 1 / 4, 1 / 2])

np.sin(angulos)

array([0.        , 0.70710678, 1.        ])

En cambio, si queremos usar la función seno del módulo math:

math.sin(angulos)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[31], line 1
----> 1 math.sin(angulos)

TypeError: only length-1 arrays can be converted to Python scalars

Si quieren ver que funciones define NumPy, pueden leer la documentación.

Ejercicio 2#

Generar un array con los 10 primeros números enteros, \(k \in \{0, 1, \ldots\}\), y calcular:

sus cuadrados: \(k^2\)
las potencias de \(2\): \(2^k\).

# Escriba aquí su solución

Solución#

Graficando funciones#

Recordemos:

Para graficar una función \(y = f(x)\) en un dado rango de \(x\), tenemos que:

elegir algunos valores \(x_i\) en ese rango,

calcular \(y_i = f(x_i)\),

graficar los puntos \((x_i, y_i)\) y unirlos con lineas.

Con estas herramientas, podemos graficar funciones muy fácilmente.

Para el primer punto, podemos usar la función np.linspace.

Para el segundo punto, aprovechamos las operaciones elemento a elemento y broadcasting de NumPy.

Para el tercer punto, vamos a usar la función plot de matplotlib.pyplot (que importamos como plt).

Por ejemplo, grafiquemos una función cuadrática:

x = np.linspace(-1, 1, 100)
y = x**2

plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x7fa814550e20>]

../_images/c5fca2a9159760da83c723e727b379dd7a156b3171bde5b2e38c19ad2b61371f.png

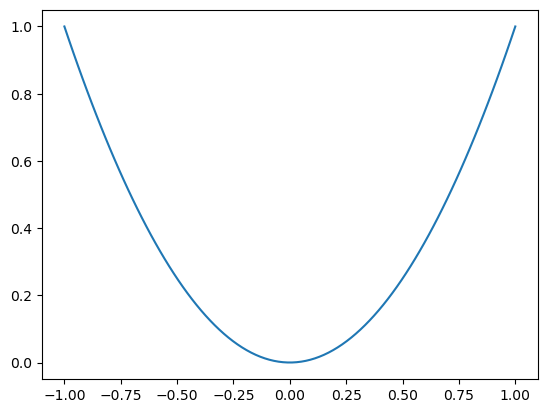
Al graficar, matplotlib grafica puntos en las posiciones (x[i], y[i]) y los une con lineas.

Esto es más claro si usamos una menor cantidad de puntos:

x = np.linspace(-1, 1, 5)
y = x**2

plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x7fa8145ae170>]

../_images/3640d83e16651d78d6fbb96993ed2c819e97f0ff5f63a92f04b403ab761d9047.png

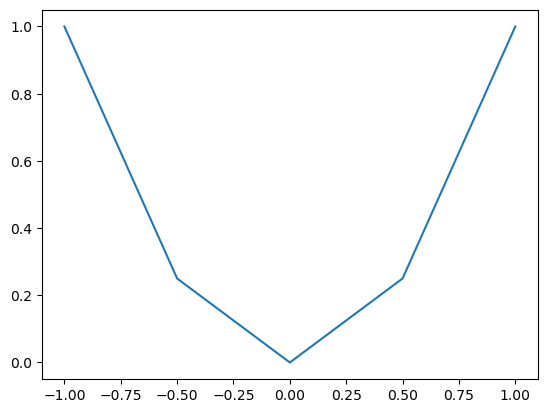
También, podemos agregar la opción marker para que dibuje los puntos:

plt.plot(x, y, marker="o")

[<matplotlib.lines.Line2D at 0x7fa814040b50>]

../_images/175f4f4635aec8aa0996ac54f31a8bb1b2ac9e4b08c78fb2d66a0f18f02d23c0.png

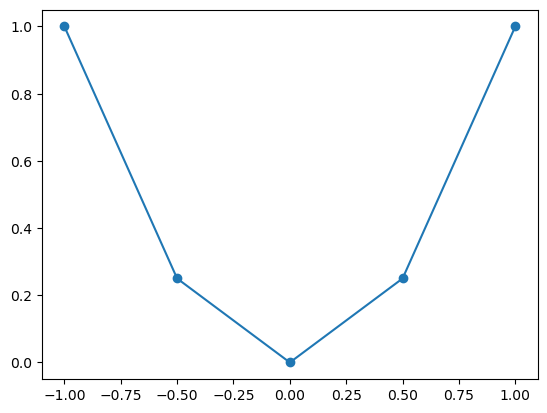
En este caso, elegimos o como marker, pero hay más variantes para elegir, que pueden consultar en la documentación.

Ejercicio 3#

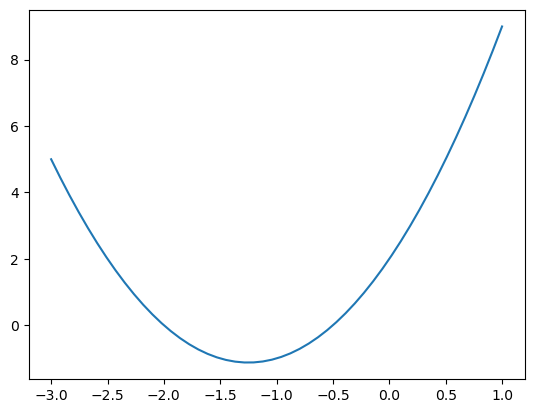
Graficar el polinomio \(f(x) = 2x^2 - 5x + 2\) en el rango \(-3 \leq x \leq 1\).

# Escriba aquí su solución

Solución#

Graficando múltiples lineas#

Para graficar múltiples lineas, se puede llamar múltiples veces a la función plt.plot.

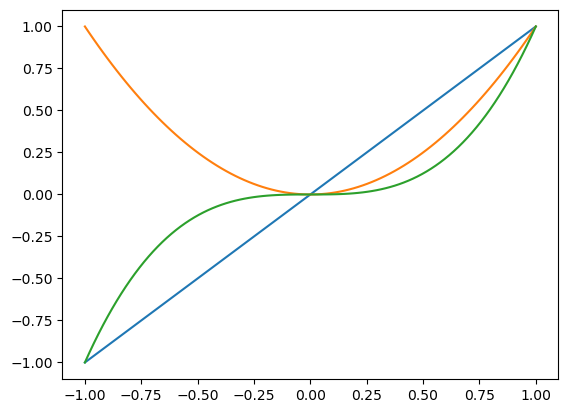
Por ejemplo,

x = np.linspace(-1, 1, 100)

plt.plot(x, x)
plt.plot(x, x**2)
plt.plot(x, x**3)

[<matplotlib.lines.Line2D at 0x7fa8140d36a0>]

../_images/842c125ae8aa07367625509c3925186c3d4a707af6c96cd0785bd8ea6b088aca.png

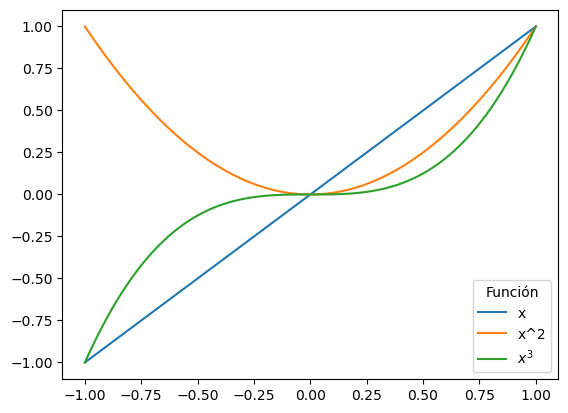
Si le damos un nombre a cada línea con el parámetro label, y podemos usar la función plt.legend para que nos muestre la leyenda:

x = np.linspace(-1, 1, 100)

plt.plot(x, x, label="x")
plt.plot(x, x**2, label="x^2")
plt.plot(x, x**3, label="$x^3$")

plt.legend(title="Función")

<matplotlib.legend.Legend at 0x7fa800d5c940>

../_images/fccd8fb3504722fa0db5a9896d1a74467d0409a31f16c1451023b33a36308025.png

Ejercicio 4#

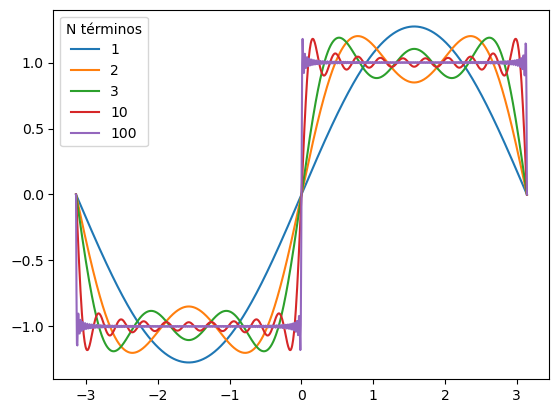
Para el rango \(x \in [-\pi, \pi]\), graficar la sumatoria:

\[ f(x) = \frac{1}{4 \pi} \sum_{k \in N \text{ impar}} \frac{\sin(k x)}{k} \]

donde la suma es sobre los números naturales impares. Es decir, \(k \in \{1, 3, 5, \ldots\}\).

Equivalentemente, se puede escribir como:

\[ f(x) = \frac{1}{4 \pi} \sum_{k=0}^n \frac{\sin\Big((2k+1) \; x\Big)}{(2k+1)} \]

para \(k \in \{0, 1, 2, \ldots\}\).

Cortar la sumatoria en diferente cantidad de términos. Por ejemplo, \(n \in \{1, 2, 3, 10, 100\}\).

# Escriba aquí su solución